Параллелограмм свойства углов сторон и диагоналей параллелограмма. Параллелограмм. Противоположные стороны тождественны

В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:

• чем признак отличается от свойства;
• рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
• сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.

2.1 Определение параллелограмма

Чтобы правильно давать определения понятиям в геометрии, нужно не просто их заучивать, а понимать, как они формируются. В этом деле нам хорошо помогают схемы родовых понятий. Давайте посмотрим, что это такое.

Наш учебный модуль называется «Четырехугольники» и четырехугольник является ключевым понятием в этом курсе. Мы можем дать следующее определение четырехугольнику:

Четырёхугольник -это многоугольник , у которого четыре стороны и четыре вершины.

В этом определении родовым понятием будет многоугольник. Теперь дадим определение многоугольнику:

Многоугольником называется простая замкнутая ломаная вместе с частью плоскости, которую она ограничивает.

Ясно, что родовым понятием здесь выступает понятие ломаная. Если мы пойдем далее, то придем к понятию отрезка, а затем к конечным понятиям точка и прямая. Таким же образом мы можем продолжить нашу схему вниз:

Если мы потребуем, чтобы у четырехугольника две стороны были параллельны, а две нет, то мы получим фигуру, которая называется трапецией.

Трапеция – четырехугольник , у которого две стороны параллельны, а две другие - не параллельны.

А в случае, когда все противоположные стороны параллельны, мы имеем дело с параллелограммом.

Параллелограмм – четырехугольник , у которого противоположные стороны параллельны.

2.2 Cвойства параллелограмма

Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

Докажем это свойство.

Дано: ABCD - параллелограмм.

Доказать: $\angle A = \angle C, \angle B = \angle D, AB = CD, AD = BC.$

Доказательство:

При доказательстве свойств любого геометрического объекта всегда вспоминаем его определение. Итак, параллелограмм – четырехугольник, у которого противоположные стороны параллельны. Ключевым моментом здесь выступает параллельность сторон.

Построим секущую ко всем четырем прямым. Такой секущей будет диагональ BD.

Очевидно, что нужно рассмотреть углы, образованные секущей и параллельными прямыми. Так как прямые параллельны, то накрест лежащие углы равны.

Теперь можно увидеть два равных треугольника по второму признаку.

Из равенства треугольников непосредственно следует первое свойство параллелограмма.

Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

Дано: ABCD - параллелограмм.

Доказать: $AO = OC, BO = OD.$

Доказательство:

Логика доказательства здесь такая же, как и в предыдущем свойстве: параллельность сторон и равенство треугольников. Первый шаг доказательства тот же, что у первого свойства.

Вторым шагом мы доказываем равенство треугольников по второму признаку. Обратите внимание, что равенство $BC=AD$ можно принять без доказательства (используя Свойство 1 ).

Из этого равенства следует, что $AO = OC, BO = OD.$

2.3 Опорная задача №4 (Свойство угла между высотами параллелограмма)

Дано: ABCD - параллелограмм, BK и BM - его высоты, $\angle KBM = 60^0$ .

Найти: $\angle ABK$, $\angle A$

Решение: Приступая к решению этой задачи, нужно иметь ввиду следующее:

высота в параллелограмме перпендикулярна обеим противоположным сторонам

Например, если отрезок $BM$ проведен к стороне $DC$ и является его высотой ($BM \perp DC$), то этот же отрезок будет высотой к противположной стороне ($BM \perp BA$). Это следует из параллельности сторон $AB \parallel DC$.

При решении этой задачи, ценным является свойство, которое мы получаем.

Дополнительное свойство. Угол между высотами параллелограмма, проведенными из его вершины, равен углу при соседней вершине.

2.4 Опорная задача №5 (Свойство биссектрисы параллелограмма)

Биссектриса угла А параллелограмма ABCD пересекает сторону BC в точке L , AD=12 см , AB =10 см . Найти длину отрезка LC .

Решение :

1. $\angle 1 = \angle 2$ (АК - биссектрисса);
2. $\angle 2 = \angle 3$ (как накрест лежащие углы при $AD \parallel BC$ и секущей АL);
3. $\angle 1 = \angle 3$, $\bigtriangleup ABL -$ равнобедренный.

По ходу решения задачи мы получили свойство:

Дополнительное свойство. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.

1 признак параллелограмма

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.

Доказательство:

Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.

Эти треугольники равны между собой по двум сторонам и углу между ними (BD - общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.

А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.

2 признак параллелограмма

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.

Доказательство:

Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.

Эти два треугольника буду равны между собой по трем сторонам (BD - общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.

3 признак параллелограмма

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.

Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.

Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.

Определение

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

На рисунке 1 изображен параллелограмм $A B C D, A B\|C D, B C\| A D$.

Свойства параллелограмма

1. В параллелограмме противоположные стороны равны: $A B=C D, B C=A D$ (рис 1).
2. В параллелограмме противоположные углы равны $\angle A=\angle C, \angle B=\angle D$ (рис 1).
3. Диагонали параллелограмма в точке пересечения делятся пополам $A O=O C, B O=O D$ (рис 1).
4. Диагональ параллелограмма делит его на два равных треугольника.

Сумма углов параллелограмма, прилежащих к одной стороне равна $180^{\circ}$:

$$\angle A+\angle B=180^{\circ}, \angle B+\angle C=180^{\circ}$$

$$\angle C+\angle D=180^{\circ}, \angle D+\angle A=180^{\circ}$$

Диагонали и стороны параллелограмма связаны следующим соотношением:

$$d_{1}^{2}+d_{2}^{2}=2 a^{2}+2 b^{2}$$

5. В параллелограмме угол между высотами равен его острому углу: $\angle K B H=\angle A$.
6. Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
7. Биссектрисы двух противоположных углов параллелограмма параллельны.

Признаки параллелограмма

Четырехугольник $ABCD$ будет параллелограммом, если

1. $A B=C D$ и $A B \| C D$
2. $A B=C D$ и $B C=A D$
3. $A O=O C$ и $B O=O D$
4. $\angle A=\angle C$ и $\angle B=\angle D$

Площадь параллелограмма можно вычислить по одной из следующих формул:

$S=a \cdot h_{a}, \quad S=b \cdot h_{b}$

$S=a \cdot b \cdot \sin \alpha, \quad S=\frac{1}{2} d_{1} \cdot d_{2} \cdot \sin \phi$

Примеры решения задач

Пример

Задание. Сумма двух углов параллелограмма равна $140^{\circ}$. Найти больший угол параллелограмма.

Решение. В параллелограмме противоположные углы равны. Обозначим больший угол параллелограмма $\alpha$, а меньший угол $\beta$. Сумма углов $\alpha$ и $\beta$ равна $180^{\circ}$, поэтому заданная сумма, равная $140^{\circ}$, это сумма двух противоположных углов, тогда $140^{\circ} : 2=70^{\circ}$. Таким образом меньший угол $\beta=70^{\circ}$. Больший угол $\alpha$ найдем из соотношения:

$\alpha+\beta=180^{\circ} \Rightarrow \alpha=180^{\circ}-\beta \Rightarrow$

$\Rightarrow \alpha=180^{\circ}-70^{\circ} \Rightarrow \alpha=110^{\circ}$

Ответ. $\alpha=110^{\circ}$

Пример

Задание. Стороны параллелограмма равны 18 см и 15 см, а высота, проведенная к меньшей стороне, равна 6 см. Найти другую высоту параллелограмма.

Решение. Сделаем рисунок (рис. 2)

По условию, $a=15$ см, $b=18$ см, $h_{a}=6$ см. Для параллелограмма справедливы следующие формулы для нахождения площади:

$$S=a \cdot h_{a}, \quad S=b \cdot h_{b}$$

Приравняем правые части этих равенств, и выразим, из полученного равенства, $h_{b} $:

$$a \cdot h_{a}=b \cdot h_{b} \Rightarrow h_{b}=\frac{a \cdot h_{a}}{b}$$

Подставляя исходные данные задачи, окончательно получим:

$h_{b}=\frac{15 \cdot 6}{18} \Rightarrow h_{b}=5$ (см)

Понятие параллелограмма

Определение 1

Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).

Рисунок 1.

Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.

Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.

Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.

Признаки параллелограмма

Рассмотрим три признака параллелограмма и представим их в виде теорем.

Теорема 1

Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).

Рисунок 2.

Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда

\[\angle CAB=\angle DCA\]

как накрест лежащие углы.

По $I$ признаку равенства треугольников,

так как $AC$ -- их общая сторона, а $AB=CD$ по условию. Значит

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 2

Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).

Рисунок 3.

Так как $AD=BC$, $AB=CD$, а $AC$ -- общая сторона, то по $III$ признаку равенства треугольников,

\[\triangle DAC=\triangle ACB\]

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

\[\angle DCA=\angle CAB\]

Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 3

Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).

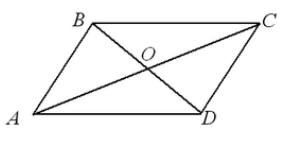
Рисунок 4.

Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.

Определение

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

Точку пересечения диагоналей параллелограмма называют его центром .

Свойства параллелограмма:

1. Сумма любых двух соседних углов параллелограмма равна $180^{\circ}$, а противоположные углы равны.
2. Противолежащие стороны параллелограмма равны.
3. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

Доказательство

Пусть дан параллелограмм $ABCD$.

1. Заметим, что соседние углы $A$ и $B$ параллелограмма являются внутренними односторонними при параллельных прямых $AD$ и $BC$ и секущей $AB$, то есть их сумма равна $180^\circ$. Аналогично для других пар углов.

Если $\angle A + \angle B=180^\circ$ и $\angle C + \angle B=180^\circ$, то $\angle A = \angle C$. Аналогично, $\angle B = \angle D$.

2. Рассмотрим треугольники $ABC$ и $CDA$. Из параллельности противоположных сторон параллелограмма следует, что $\angle BAC=\angle DCA$ и $\angle BCA=\angle DAC$. Поскольку $AC$ - общая, то треугольники $ABC$ и $CDA$ равны по второму признаку. Из равенства треугольников следует, что $AB=CD$ и $BC=AD$.

3. Поскольку параллелограмм - выпуклый четырехугольник, то его диагонали пересекаются. Пусть $O$ - точка пересечения. Из параллельности сторон $BC$ и $AD$ параллелограмма следует, что $\angle OAD=\angle OCB$ и $\angle ODA=\angle OBC$. Учитывая равенство $BC=AD$ получим, что треугольники $AOD$ и $COB$ равны по второму признаку. Следовательно, $AO=CO$ и $DO=BO$, что и требовалось.

Признаки параллелограмма:

1. Если в четырехугольнике сумма любых двух соседних углов равна $180^{\circ}$, то этот четырехугольник - параллелограмм.
2. Если в четырехугольнике противолежащие углы попарно равны, то этот четырехугольник - параллелограмм.
3. Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник - параллелограмм.
4. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.
5. Если диагонали четырехугольника делятся точкой их пересечения пополам, то этот четырехугольник - параллелограмм.

Доказательство

Пусть дан четырехугольник $ABCD$.

1. Заметим, что соседние углы $A$ и $B$ являются внутренними односторонними при прямых $AD$ и $BC$ и секущей $AB$. Так как их сумма равна $180^\circ$, то прямые $AD$ и $BC$ параллельны. Аналогично для другой пары прямых, то есть $ABCD$ - параллелограмм по определению.

2. Заметим, что $\angle A + \angle B + \angle C + \angle D=360^\circ$. Если $\angle A = \angle C$, а $\angle B = \angle D$, то $\angle A + \angle B=180^\circ$ и аналогично для других пар соседних углов. Далее используем предыдущий признак.

3. Рассмотрим треугольники $ABC$ и $CDA$. Поскольку $AC$ - общая, то из равенства противоположных сторон параллелограмма следует, что треугольники $ABC$ и $CDA$ равны по третьему признаку. Следовательно, $\angle BAC=\angle DCA$ и $\angle BCA=\angle DAC$, откуда следует параллельность противолежащих сторон.

4. Пусть $BC$ и $AD$ равны и параллельны. Рассмотрим треугольники $ABC$ и $CDA$. Из параллельности прямых следует, что $\angle BCA=\angle DAC$. Поскольку $AC$ - общая и $BC=AD$, то треугольники $ABC$ и $CDA$ равны по первому признаку. Следовательно, $AB=CD$. Далее используем предыдущий признак.

5. Пусть $O$ - точка пересечения диагоналей и $AO=CO$, а $DO=BO$.Учитывая равенство вертикальных углов, получим, что треугольники $AOD$ и $COB$ равны по первому признаку. Следовательно, $\angle OAD=\angle OCB$, откуда следует параллельность $BC$ и $AD$. Аналогично для другой пары сторон.

Определение

Четырехугольник, в котором есть три прямых угла, называется прямоугольником.

Свойства прямоугольника:

1. Диагонали прямоугольника равны.

Доказательство

Пусть дан прямоугольник $ABCD$. Поскольку прямоугольник является параллелограммом, то его противолежащие стороны равны. Тогда прямоугольные треугольники $ABD$ и $DCA$ равны по двум катетам, откуда следует, что $BD=AC$.

Признаки прямоугольника:

1. Если в параллелограмме есть прямой угол, то этот параллелограмм является прямоугольником.
2. Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.

Доказательство

1. Если один из углов параллелограмма прямой, то, учитывая, что сумма соседних углов равна $180^{\circ}$, получим, что прямыми являются и остальные углы.

2. Пусть в параллелограмме $ABCD$ диагонали $AC$ и $BD$ равны. Учитывая равенство противолежащих сторон $AB$ и $DC$, получим, что треугольники $ABD$ и $DCA$ равны по третьему признаку. Следовательно, $\angle BAD=\angle CDA$, то есть они прямые. Осталось воспользоваться предыдущим признаком.

Определение

Четырехугольник, в котором все стороны равны, называется ромбом.

Свойства ромба:

1. Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.

Доказательство

Пусть в ромбе $ABCD$ диагонали $AC$ и $BD$ пересекаются в точке $O$. Так как ромб является параллелограммом, то $AO=OC$. Рассмотрим равнобедренный треугольник $ABC$. Так как $AO$ - медиана проведнная к основанию, то она является биссектрисой и высотой, что и требовалось.

Признаки ромба:

1. Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм является ромбом.
2. Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм является ромбом.

Доказательство

Пусть в параллелограмме $ABCD$ диагонали $AC$ и $BD$ пересекаются в точке $O$. Рассмотрим треугольник $ABC$.

1. Если диагонали перпендикулярны, то $BO$ является в треугольнике медианой и высотой.

2. Если диагональ $BD$ содержит биссектрису угла $ABC$, то $BO$ является в треугольнике медианой и биссектрисой.

В обоих случаях получим, что треугольник $ABC$ - равнобедренный и в параллелограмме соседние стороны равны. Следовательно, он является ромбом, что и требовалось.

Определение

Прямоугольник, у которого две соседние стороны равны, называется квадратом.

Признаки квадрата:

1. Если у ромба есть прямой угол, то этот ромб является квадратом.
2. Если у ромба диагонали равны, то этот ромб является квадратом.

Доказательство

Если у параллелограмма есть прямой угол или равны диагонали, то он является прямоугольником. Если же четырехугольник является прямоугольником и ромбом, то он - квадрат.