Παραλληλόγραμμες ιδιότητες των γωνιών των πλευρών και των διαγωνίων ενός παραλληλογράμμου. Παραλληλόγραμμο. Οι απέναντι πλευρές είναι ίδιες

Σε αυτή την ενότητα εξετάζουμε το παραλληλόγραμμο του γεωμετρικού αντικειμένου. Όλα τα στοιχεία ενός παραλληλογράμμου κληρονομούνται από ένα τετράπλευρο, επομένως δεν θα τα εξετάσουμε. Αλλά οι ιδιότητες και τα χαρακτηριστικά αξίζουν λεπτομερούς εξέτασης. Θα εξετάσουμε:

• σε τι διαφέρει ένα σημάδι από ένα ακίνητο;
• Ας δούμε τις βασικές ιδιότητες και χαρακτηριστικά που μελετώνται στο πρόγραμμα της 8ης τάξης.
• Ας διατυπώσουμε δύο επιπλέον ιδιότητες που λαμβάνουμε κατά την επίλυση προβλημάτων υποστήριξης.

2.1 Ορισμός παραλληλογράμμου

Για να ορίσετε σωστά τις έννοιες στη γεωμετρία, δεν χρειάζεται απλώς να τις απομνημονεύσετε, αλλά να κατανοήσετε πώς σχηματίζονται. Σε αυτό το θέμα, τα σχήματα γενικών εννοιών μας βοηθούν καλά. Ας δούμε τι είναι.

Η εκπαιδευτική μας ενότητα ονομάζεται "Τετράπλευρα" και το τετράπλευρο είναι βασική έννοια σε αυτό το μάθημα. Μπορούμε να δώσουμε τον ακόλουθο ορισμό του τετράπλευρου:

Τετράπλευρο-Αυτό πολύγωνο, που έχει τέσσερις πλευρές και τέσσερις κορυφές.

Σε αυτόν τον ορισμό, η γενική έννοια θα είναι ένα πολύγωνο. Τώρα ας ορίσουμε ένα πολύγωνο:

Πολύγωνοονομάζεται απλός κλειστός σπασμένη γραμμήμαζί με το τμήμα του αεροπλάνου που δεσμεύει.

Είναι σαφές ότι η γενική έννοια εδώ είναι η έννοια της διακεκομμένης γραμμής. Αν προχωρήσουμε παραπέρα, θα φτάσουμε στην έννοια του τμήματος και μετά στις τελικές έννοιες ενός σημείου και μιας ευθείας γραμμής. Με τον ίδιο τρόπο μπορούμε να συνεχίσουμε το διάγραμμά μας προς τα κάτω:

Αν απαιτήσουμε δύο πλευρές ενός τετράπλευρου να είναι παράλληλες και δύο όχι, τότε παίρνουμε ένα σχήμα που ονομάζεται τραπέζιο.

Τραπεζοειδές – τετράπλευρο, στο οποίο δύο πλευρές είναι παράλληλες και οι άλλες δύο δεν είναι παράλληλες.

Και στην περίπτωση που όλες οι απέναντι πλευρές είναι παράλληλες, έχουμε να κάνουμε με παραλληλόγραμμο.

Παραλληλόγραμμο – τετράπλευρο, του οποίου οι απέναντι πλευρές είναι παράλληλες.

2.2 Ιδιότητες παραλληλογράμμου

Ιδιοκτησία 1.Σε ένα παραλληλόγραμμο, οι απέναντι πλευρές είναι ίσες και οι απέναντι γωνίες είναι ίσες.

Ας αποδείξουμε αυτή την ιδιότητα.

Δεδομένος:Το ABCD είναι παραλληλόγραμμο.

Αποδεικνύω:$\γωνία A = \γωνία C, \γωνία B = \γωνία D, AB = CD, AD = BC.$

Απόδειξη:

Όταν αποδεικνύουμε τις ιδιότητες οποιουδήποτε γεωμετρικού αντικειμένου, θυμόμαστε πάντα τον ορισμό του. Ετσι, παραλληλόγραμμο- ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες. Το βασικό σημείο εδώ είναι ο παραλληλισμός των πλευρών.

Ας κατασκευάσουμε μια τομή και στις τέσσερις γραμμές. Αυτή η τομή θα είναι η διαγώνιος BD.

Προφανώς, πρέπει να εξετάσουμε τις γωνίες που σχηματίζονται από τις εγκάρσιες και παράλληλες ευθείες. Δεδομένου ότι οι ευθείες είναι παράλληλες, οι γωνίες που βρίσκονται κατά μήκος τους είναι ίσες.

Τώρα μπορείτε να δείτε δύο ίσα τρίγωνα σύμφωνα με το δεύτερο σημάδι.

Η ισότητα των τριγώνων συνεπάγεται άμεσα την πρώτη ιδιότητα ενός παραλληλογράμμου.

Ιδιοκτησία 2.Οι διαγώνιοι ενός παραλληλογράμμου διαιρούνται στο μισό με το σημείο τομής.

Δεδομένος: Α Β Γ Δ- παραλληλόγραμμο.

Αποδεικνύω:$AO = OC, BO = OD.$

Απόδειξη:

Η λογική της απόδειξης εδώ είναι η ίδια με την προηγούμενη ιδιότητα: παραλληλισμός πλευρών και ισότητα τριγώνων. Το πρώτο βήμα της απόδειξης είναι το ίδιο με το πρώτο ακίνητο.

Το δεύτερο βήμα είναι να αποδείξουμε την ισότητα των τριγώνων με το δεύτερο κριτήριο. Λάβετε υπόψη ότι η ισότητα $BC=AD$ μπορεί να γίνει αποδεκτή χωρίς απόδειξη (χρησιμοποιώντας Ιδιοκτησία 1).

Από αυτή την ισότητα προκύπτει ότι $AO = OC, BO = OD.$

2.3 Πρόβλημα στήριξης Νο. 4 (Ιδιότητα της γωνίας μεταξύ των υψών ενός παραλληλογράμμου)

Δεδομένος: Α Β Γ Δ - παραλληλόγραμμο, B.K. Και Β.Μ. - το ύψος του, $\γωνία KBM = 60^0$.

Εύρημα:$\γωνία ABK$, $\γωνία A$

Λύση:Όταν ξεκινάτε να επιλύετε αυτό το πρόβλημα, πρέπει να έχετε υπόψη σας τα εξής:

το ύψος σε ένα παραλληλόγραμμο είναι κάθετο και στις δύο απέναντι πλευρές

Για παράδειγμα, εάν ένα τμήμα $BM$ σχεδιάζεται στην πλευρά $DC$ και είναι το ύψος του ($BM \perp DC$), τότε το ίδιο τμήμα θα είναι το ύψος στην αντίθετη πλευρά ($BM \perp BA$). Αυτό προκύπτει από τον παραλληλισμό των πλευρών $AB \parallel DC$.

Κατά την επίλυση αυτού του προβλήματος, η ιδιοκτησία που αποκτάμε είναι πολύτιμη.

Πρόσθετο ακίνητο.Η γωνία μεταξύ των υψομέτρων ενός παραλληλογράμμου που αντλείται από την κορυφή του είναι ίση με τη γωνία στη διπλανή κορυφή.

2.4 Πρόβλημα υποστήριξης Νο. 5 (Ιδιότητα διχοτόμου παραλληλογράμμου)

Διχοτόμος γωνίας ΕΝΑπαραλληλόγραμμο Α Β Γ Δδιασχίζει το πλάι ΠΡΟ ΧΡΙΣΤΟΥ.στο σημείο μεγάλο, μ.Χ.=12 εκ, AB =10 cm. Βρείτε το μήκος του τμήματος L.C..

Λύση:

1. $\γωνία 1 = \γωνία 2$ (AK - διχοτόμος);
2. $\γωνία 2 = \γωνία 3$ (ως εγκάρσιες γωνίες με $AD \παράλληλη BC$ και τέμνουσα AL);
3. $\γωνία 1 = \γωνία 3$, $\μεγάλο τρίγωνο ABL -$ ισοσκελές.

Κατά την επίλυση του προβλήματος, αποκτήσαμε την ακόλουθη ιδιότητα:

Πρόσθετο ακίνητο.Η διχοτόμος της γωνίας ενός παραλληλογράμμου αποκόπτει ένα ισοσκελές τρίγωνο από αυτό.

Προκειμένου να καθοριστεί εάν ένα δεδομένο σχήμα είναι παραλληλόγραμμο, υπάρχουν πολλά σημάδια. Ας δούμε τα τρία κύρια χαρακτηριστικά ενός παραλληλογράμμου.

1 παραλληλόγραμμο σημάδι

Αν δύο πλευρές ενός τετράπλευρου είναι ίσες και παράλληλες, τότε αυτό το τετράπλευρο θα είναι παραλληλόγραμμο.

Απόδειξη:

Θεωρήστε το τετράπλευρο ABCD. Έστω παράλληλες οι πλευρές ΑΒ και ΓΔ. Και ας AB=CD. Ας σχεδιάσουμε τη διαγώνιο BD σε αυτό. Θα χωρίσει αυτό το τετράπλευρο σε δύο ίσα τρίγωνα: ABD και CBD.

Αυτά τα τρίγωνα είναι ίσα μεταξύ τους κατά μήκος δύο πλευρών και η μεταξύ τους γωνία (BD είναι η κοινή πλευρά, AB = CD κατά συνθήκη, γωνία 1 = γωνία2 ως εγκάρσιες γωνίες με το εγκάρσιο BD των παράλληλων ευθειών AB και CD.) και επομένως γωνία3 = γωνία 4.

Και αυτές οι γωνίες θα βρίσκονται εγκάρσια όταν οι ευθείες BC και AD τέμνονται με την τέμνουσα BD. Από αυτό προκύπτει ότι π.Χ. και μ.Χ. είναι παράλληλες μεταξύ τους. Έχουμε ότι στο τετράπλευρο ΑΒΓΔ οι απέναντι πλευρές είναι κατά ζεύγη παράλληλες, και επομένως το τετράπλευρο ΑΒΓΔ είναι παραλληλόγραμμο.

Παραλληλόγραμμο σημάδι 2

Αν σε ένα τετράπλευρο οι απέναντι πλευρές είναι ίσες σε ζεύγη, τότε αυτό το τετράπλευρο θα είναι παραλληλόγραμμο.

Απόδειξη:

Θεωρήστε το τετράπλευρο ABCD. Ας σχεδιάσουμε τη διαγώνιο BD σε αυτό. Θα χωρίσει αυτό το τετράπλευρο σε δύο ίσα τρίγωνα: ABD και CBD.

Αυτά τα δύο τρίγωνα θα είναι ίσα μεταξύ τους σε τρεις πλευρές (BD είναι η κοινή πλευρά, AB = CD και BC = AD κατά συνθήκη). Από αυτό μπορούμε να συμπεράνουμε ότι γωνία1 = γωνία2. Από αυτό προκύπτει ότι το ΑΒ είναι παράλληλο με το CD. Και εφόσον AB = CD και το AB είναι παράλληλο με το CD, τότε σύμφωνα με το πρώτο κριτήριο ενός παραλληλογράμμου, το τετράπλευρο ABCD θα είναι παραλληλόγραμμο.

3 παραλληλόγραμμο σημάδι

Αν οι διαγώνιοι ενός τετράπλευρου τέμνονται και διχοτομούνται από το σημείο τομής, τότε αυτό το τετράπλευρο θα είναι παραλληλόγραμμο.

Θεωρήστε το τετράπλευρο ABCD. Ας σχεδιάσουμε δύο διαγώνιους AC και BD σε αυτό, οι οποίες θα τέμνονται στο σημείο Ο και θα διχοτομούνται από αυτό το σημείο.

Τα τρίγωνα AOB και COD θα είναι ίσα μεταξύ τους, σύμφωνα με το πρώτο πρόσημο της ισότητας των τριγώνων. (AO = OC, BO = OD κατά συνθήκη, γωνία AOB = γωνία COD ως κατακόρυφες γωνίες.) Επομένως, AB = CD και γωνία1 = γωνία 2. Από την ισότητα των γωνιών 1 και 2, έχουμε ότι το AB είναι παράλληλο προς το CD. Τότε έχουμε ότι στο τετράπλευρο ΑΒΓΔ οι πλευρές ΑΒ είναι ίσες με ΓΔ και παράλληλες, και σύμφωνα με το πρώτο κριτήριο ενός παραλληλογράμμου, το τετράπλευρο ΑΒΓΔ θα είναι παραλληλόγραμμο.

Ορισμός

Παραλληλόγραμμοείναι ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες ανά ζεύγη.

Το σχήμα 1 δείχνει το παραλληλόγραμμο $A B C D, A B\|C D, B C\| A D$.

Ιδιότητες παραλληλογράμμου

1. Σε ένα παραλληλόγραμμο, οι απέναντι πλευρές είναι ίσες: $A B=C D, B C=A D$ (Εικόνα 1).
2. Σε ένα παραλληλόγραμμο, οι απέναντι γωνίες είναι ίσες με $\γωνία A=\γωνία C, \γωνία B=\γωνία D$ (Εικόνα 1).
3. Οι διαγώνιοι του παραλληλογράμμου στο σημείο τομής χωρίζονται στο μισό $A O=O C, B O=O D$ (Εικόνα 1).
4. Η διαγώνιος ενός παραλληλογράμμου το χωρίζει σε δύο ίσα τρίγωνα.

Το άθροισμα των γωνιών ενός παραλληλογράμμου δίπλα στη μία πλευρά είναι $180^(\circ)$:

$$\γωνία A+\γωνία B=180^(\circ), \γωνία B+\γωνία C=180^(\circ)$$

$$\γωνία C+\γωνία D=180^(\circ), \γωνία D+\γωνία A=180^(\circ)$$

Οι διαγώνιοι και οι πλευρές ενός παραλληλογράμμου σχετίζονται με την ακόλουθη σχέση:

$$d_(1)^(2)+d_(2)^(2)=2 a^(2)+2 b^(2)$$

5. Σε ένα παραλληλόγραμμο, η γωνία μεταξύ των υψομέτρων είναι ίση με την οξεία γωνία του: $\γωνία K B H=\γωνία A$.
6. Οι διχοτόμοι των γωνιών που γειτνιάζουν με τη μία πλευρά ενός παραλληλογράμμου είναι αμοιβαία κάθετες.
7. Οι διχοτόμοι δύο απέναντι γωνιών ενός παραλληλογράμμου είναι παράλληλες.

Σημάδια παραλληλογράμμου

Το τετράπλευρο $ABCD$ είναι παραλληλόγραμμο αν

1. $A B=C D$ και $A B \| C D$
2. $A B=C D$ και $B C=A D$
3. $A O=O C$ και $B O=O D$
4. $\γωνία A=\γωνία C$ και $\γωνία B=\γωνία D$

Το εμβαδόν ενός παραλληλογράμμου μπορεί να υπολογιστεί χρησιμοποιώντας έναν από τους παρακάτω τύπους:

$S=a \cdot h_(a), \quad S=b \cdot h_(b)$

$S=a \cdot b \cdot \sin \alpha, \quad S=\frac(1)(2) d_(1) \cdot d_(2) \cdot \sin \phi$

Παραδείγματα επίλυσης προβλημάτων

Παράδειγμα

Ασκηση.Το άθροισμα δύο γωνιών ενός παραλληλογράμμου είναι $140^(\circ)$. Να βρείτε τη μεγαλύτερη γωνία του παραλληλογράμμου.

Λύση.Σε ένα παραλληλόγραμμο οι απέναντι γωνίες είναι ίσες. Ας συμβολίσουμε τη μεγαλύτερη γωνία του παραλληλογράμμου ως $\alpha$ και τη μικρότερη γωνία ως $\beta$. Το άθροισμα των γωνιών $\alpha$ και $\beta$ είναι $180^(\circ)$, επομένως ένα δεδομένο άθροισμα ίσο με $140^(\circ)$ είναι το άθροισμα δύο απέναντι γωνιών, στη συνέχεια $140^(\circ) : 2=70 ^(\circ)$. Έτσι η μικρότερη γωνία είναι $\beta=70^(\circ)$. Βρίσκουμε τη μεγαλύτερη γωνία $\alpha$ από τη σχέση:

$\alpha+\beta=180^(\circ) \Rightarrow \alpha=180^(\circ)-\beta \Rightarrow$

$\Rightarrow \alpha=180^(\circ)-70^(\circ) \Rightarrow \alpha=110^(\circ)$

Απάντηση.$\alpha=110^(\circ)$

Παράδειγμα

Ασκηση.Οι πλευρές του παραλληλογράμμου είναι 18 cm και 15 cm, και το ύψος που τραβιέται στη μικρότερη πλευρά είναι 6 cm.

Λύση.Ας κάνουμε ένα σχέδιο (Εικ. 2)

Σύμφωνα με τη συνθήκη, $a=15$ cm, $b=18$ cm, $h_(a)=6$ cm, ισχύουν οι ακόλουθοι τύποι για την εύρεση του εμβαδού:

$$S=a \cdot h_(a), \quad S=b \cdot h_(b)$$

Ας εξισώσουμε τις δεξιές πλευρές αυτών των ισοτήτων και ας εκφράσουμε, από την προκύπτουσα ισότητα, $h_(b) $:

$$a \cdot h_(a)=b \cdot h_(b) \Δεξί βέλος h_(b)=\frac(a \cdot h_(a))(b)$$

Αντικαθιστώντας τα αρχικά δεδομένα του προβλήματος, τελικά παίρνουμε:

$h_(b)=\frac(15 \cdot 6)(18) \Δεξί βέλος h_(b)=5$ (cm)

Έννοια παραλληλογράμμου

Ορισμός 1

Παραλληλόγραμμοείναι ένα τετράπλευρο στο οποίο οι απέναντι πλευρές είναι παράλληλες μεταξύ τους (Εικ. 1).

Εικόνα 1.

Ένα παραλληλόγραμμο έχει δύο κύριες ιδιότητες. Ας τα εξετάσουμε χωρίς αποδείξεις.

Ιδιοκτησία 1: Οι απέναντι πλευρές και γωνίες ενός παραλληλογράμμου είναι ίσες, αντίστοιχα.

Ιδιοκτησία 2: Οι διαγώνιες που σχεδιάζονται σε ένα παραλληλόγραμμο διχοτομούνται από το σημείο τομής τους.

Σημάδια παραλληλογράμμου

Ας εξετάσουμε τρία χαρακτηριστικά ενός παραλληλογράμμου και ας τα παρουσιάσουμε με τη μορφή θεωρημάτων.

Θεώρημα 1

Αν δύο πλευρές ενός τετράπλευρου είναι ίσες μεταξύ τους και επίσης παράλληλες, τότε αυτό το τετράπλευρο θα είναι παραλληλόγραμμο.

Απόδειξη.

Ας μας δοθεί ένα τετράπλευρο $ABCD$. Στο οποίο $AB||CD$ και $AB=CD$ Ας σχεδιάσουμε μια διαγώνιο $AC$ σε αυτό (Εικ. 2).

Σχήμα 2.

Εξετάστε τις παράλληλες ευθείες $AB$ και $CD$ και τη διατομή τους $AC$. Επειτα

\[\γωνία CAB=\γωνία DCA\]

σαν σταυρωτές γωνίες.

Σύμφωνα με το κριτήριο $I$ ισότητας τριγώνων,

αφού το $AC$ είναι η κοινή τους πλευρά και το $AB=CD$ κατά συνθήκη. Που σημαίνει

\[\γωνία DAC=\γωνία ACB\]

Εξετάστε τις ευθείες $AD$ και $CB$ και την τέμνουσα $AC$ με την τελευταία ισότητα στις κείνουσες γωνίες που λαμβάνουμε ότι $AD||CB$.) Συνεπώς, εξ ορισμού $1$, αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Το θεώρημα έχει αποδειχθεί.

Θεώρημα 2

Αν οι απέναντι πλευρές ενός τετράπλευρου είναι ίσες μεταξύ τους, τότε είναι παραλληλόγραμμο.

Απόδειξη.

Ας μας δοθεί ένα τετράπλευρο $ABCD$. Στο οποίο $AD=BC$ και $AB=CD$. Ας σχεδιάσουμε μια διαγώνιο $AC$ σε αυτό (Εικ. 3).

Εικόνα 3.

Εφόσον τα $AD=BC$, $AB=CD$ και $AC$ είναι μια κοινή πλευρά, τότε με το κριτήριο $III$ για την ισότητα των τριγώνων,

\[\τρίγωνο DAC=\τρίγωνο ACB\]

\[\γωνία DAC=\γωνία ACB\]

Ας εξετάσουμε τις ευθείες $AD$ και $CB$ και την τέμνουσα $AC$ από την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται στο $AD||CB$. Επομένως, εξ ορισμού $1$, αυτό το τετράπλευρο είναι παραλληλόγραμμο.

\[\γωνία DCA=\γωνία CAB\]

Ας εξετάσουμε τις ευθείες $AB$ και $CD$ και την τέμνουσα $AC$ με την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται στο $AB||CD$. Επομένως, σύμφωνα με τον ορισμό 1, αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Το θεώρημα έχει αποδειχθεί.

Θεώρημα 3

Αν οι διαγώνιοι που σχεδιάζονται σε ένα τετράπλευρο χωρίζονται σε δύο ίσα μέρη από το σημείο τομής τους, τότε αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Απόδειξη.

Ας μας δοθεί ένα τετράπλευρο $ABCD$. Ας σχεδιάσουμε τις διαγώνιες $AC$ και $BD$ σε αυτό. Αφήστε τα να τέμνονται στο σημείο $O$ (Εικ. 4).

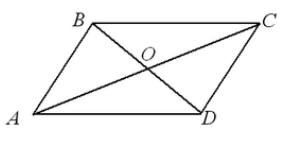
Εικόνα 4.

Εφόσον, κατά συνθήκη, $BO=OD,\ AO=OC$, και οι γωνίες $\γωνία COB=\γωνία DOA$ είναι κάθετες, τότε, με το κριτήριο $I$ για την ισότητα των τριγώνων,

\[\τρίγωνο BOC=\τρίγωνο AOD\]

\[\γωνία DBC=\γωνία BDA\]

Θεωρήστε τις ευθείες $BC$ και $AD$ και την τέμνουσα $BD$ με την τελευταία ισότητα κατά μήκος των γωνιών που βρίσκονται σε αυτό το $BC||AD$. Επίσης $BC=AD$. Επομένως, σύμφωνα με το Θεώρημα $1$, αυτό το τετράπλευρο είναι παραλληλόγραμμο.

Ορισμός

Παραλληλόγραμμοείναι ένα τετράπλευρο του οποίου οι απέναντι πλευρές είναι παράλληλες ανά ζεύγη.

Το σημείο τομής των διαγωνίων ενός παραλληλογράμμου ονομάζεται κέντρο.

Ιδιότητες παραλληλογράμμου:

1. Το άθροισμα οποιωνδήποτε δύο γειτονικών γωνιών ενός παραλληλογράμμου είναι $180^(\circ)$ και οι απέναντι γωνίες είναι ίσες.
2. Οι απέναντι πλευρές ενός παραλληλογράμμου είναι ίσες.
3. Οι διαγώνιοι ενός παραλληλογράμμου τέμνονται και διχοτομούνται στο σημείο τομής.

Απόδειξη

Έστω ένα παραλληλόγραμμο $ABCD$.

1. Σημειώστε ότι οι γειτονικές γωνίες $A$ και $B$ ενός παραλληλογράμμου είναι μονόπλευρες εσωτερικές γωνίες με παράλληλες ευθείες $AD$ και $BC$ και μια τέμνουσα $AB$, δηλαδή το άθροισμά τους είναι ίσο με $180^ \circ$. Το ίδιο και για άλλα ζεύγη γωνιών.

Αν $\γωνία A + \γωνία B=180^\circ$ και $\γωνία C + \γωνία B=180^\circ$, τότε $\γωνία A = \γωνία C$. Ομοίως, $\γωνία B = \γωνία D$.

2. Θεωρήστε τα τρίγωνα $ABC$ και $CDA$. Από τον παραλληλισμό απέναντι πλευρών ενός παραλληλογράμμου προκύπτει ότι $\γωνία BAC=\γωνία DCA$ και $\γωνία BCA=\γωνία DAC$. Εφόσον το $AC$ είναι κοινό, τότε τα τρίγωνα $ABC$ και $CDA$ είναι ίσα σύμφωνα με το δεύτερο κριτήριο. Από την ισότητα των τριγώνων προκύπτει ότι $AB=CD$ και $BC=AD$.

3. Εφόσον ένα παραλληλόγραμμο είναι κυρτό τετράπλευρο, οι διαγώνιες του τέμνονται. Έστω $O$ το σημείο τομής. Από τον παραλληλισμό των πλευρών $BC$ και $AD$ του παραλληλογράμμου προκύπτει ότι $\γωνία OAD=\γωνία OCB$ και $\γωνία ODA=\γωνία OBC$. Λαμβάνοντας υπόψη την ισότητα $BC=AD$, προκύπτει ότι τα τρίγωνα $AOD$ και $COB$ είναι ίσα σύμφωνα με το δεύτερο κριτήριο. Επομένως, $AO=CO$ και $DO=BO$, όπως απαιτείται.

Σημάδια παραλληλογράμμου:

1. Αν σε ένα τετράπλευρο το άθροισμα οποιωνδήποτε δύο γειτονικών γωνιών είναι $180^(\circ)$, τότε αυτό το τετράπλευρο είναι παραλληλόγραμμο.
2. Αν σε ένα τετράπλευρο οι απέναντι γωνίες είναι ίσες ανά ζεύγη, τότε αυτό το τετράπλευρο είναι παραλληλόγραμμο.
3. Αν σε ένα τετράπλευρο οι απέναντι πλευρές είναι ίσες σε ζευγάρια, τότε αυτό το τετράπλευρο είναι παραλληλόγραμμο.
4. Αν δύο πλευρές ενός τετράπλευρου είναι ίσες και παράλληλες, τότε το τετράπλευρο είναι παραλληλόγραμμο.
5. Αν οι διαγώνιοι ενός τετράπλευρου διχοτομούνται από το σημείο τομής τους, τότε το τετράπλευρο είναι παραλληλόγραμμο.

Απόδειξη

Έστω $ABCD$ τετράπλευρο.

1. Σημειώστε ότι οι γειτονικές γωνίες $A$ και $B$ είναι μονόπλευρες εσωτερικές γωνίες με ευθείες γραμμές $AD$ και $BC$ και εγκάρσιες $AB$. Εφόσον το άθροισμά τους είναι $180^\circ$, τότε οι ευθείες $AD$ και $BC$ είναι παράλληλες. Ομοίως για ένα άλλο ζεύγος γραμμών, δηλαδή, το $ABCD$ είναι ένα παραλληλόγραμμο εξ ορισμού.

2. Σημειώστε ότι $\γωνία A + \γωνία B + \γωνία C + \γωνία D=360^\circ$. Αν $\γωνία A = \γωνία C$, και $\γωνία B = \γωνία D$, τότε $\γωνία A + \γωνία B=180^\circ$ και ομοίως για άλλα ζεύγη γειτονικών γωνιών. Στη συνέχεια χρησιμοποιούμε το προηγούμενο σημάδι.

3. Θεωρήστε τα τρίγωνα $ABC$ και $CDA$. Εφόσον το $AC$ είναι κοινό, από την ισότητα των απέναντι πλευρών του παραλληλογράμμου προκύπτει ότι τα τρίγωνα $ABC$ και $CDA$ είναι ίσα σύμφωνα με το τρίτο κριτήριο. Επομένως, $\γωνία BAC=\γωνία DCA$ και $\γωνία BCA=\γωνία DAC$, που υποδηλώνει τον παραλληλισμό των απέναντι πλευρών.

4. Έστω $BC$ και $AD$ ίσα και παράλληλα. Εξετάστε τα τρίγωνα $ABC$ και $CDA$. Από τον παραλληλισμό των ευθειών προκύπτει ότι $\γωνία BCA=\γωνία DAC$. Εφόσον το $AC$ είναι γενικό και το $BC=AD$, τότε τα τρίγωνα $ABC$ και $CDA$ είναι ίσα σύμφωνα με το πρώτο κριτήριο. Επομένως, $AB=CD$. Στη συνέχεια χρησιμοποιούμε το προηγούμενο σημάδι.

5. Έστω $O$ το σημείο τομής των διαγωνίων και $AO=CO$, και $DO=BO$ Λαμβάνοντας υπόψη την ισότητα των κατακόρυφων γωνιών, προκύπτει ότι τα τρίγωνα $AOD$ και $COB$. είναι ίσες σύμφωνα με το πρώτο κριτήριο. Επομένως, $\γωνία OAD=\γωνία OCB$, που συνεπάγεται τον παραλληλισμό των $BC$ και $AD$. Το ίδιο και για το άλλο ζευγάρι πλευρών.

Ορισμός

Ένα τετράπλευρο που έχει τρεις ορθές γωνίες ονομάζεται ορθογώνιο παραλληλόγραμμο.

Ιδιότητες ορθογωνίου:

1. Οι διαγώνιοι ενός ορθογωνίου είναι ίσες.

Απόδειξη

Ας δοθεί ένα ορθογώνιο $ABCD$. Δεδομένου ότι το παραλληλόγραμμο είναι παραλληλόγραμμο, οι απέναντι πλευρές του είναι ίσες. Τότε τα ορθογώνια τρίγωνα $ABD$ και $DCA$ είναι ίσα σε δύο σκέλη, πράγμα που σημαίνει ότι $BD=AC$.

Χαρακτηριστικά ενός ορθογωνίου:

1. Αν ένα παραλληλόγραμμο έχει ορθή γωνία, τότε αυτό το παραλληλόγραμμο είναι ορθογώνιο.
2. Αν οι διαγώνιοι ενός παραλληλογράμμου είναι ίσες, τότε αυτό το παραλληλόγραμμο είναι ορθογώνιο.

Απόδειξη

1. Αν μία από τις γωνίες ενός παραλληλογράμμου είναι ευθεία, τότε, λαμβάνοντας υπόψη ότι το άθροισμα των γειτονικών γωνιών είναι $180^(\circ)$, παίρνουμε ότι και οι υπόλοιπες γωνίες είναι ευθείες.

2. Έστω οι διαγώνιοι $AC$ και $BD$ ίσες στο παραλληλόγραμμο $ABCD$. Λαμβάνοντας υπόψη την ισότητα των απέναντι πλευρών $AB$ και $DC$, προκύπτει ότι τα τρίγωνα $ABD$ και $DCA$ είναι ίσα σύμφωνα με το τρίτο κριτήριο. Επομένως, $\γωνία BAD=\γωνία CDA$, δηλαδή, είναι ευθείες. Απομένει να χρησιμοποιήσετε το προηγούμενο σημάδι.

Ορισμός

Ένα τετράπλευρο στο οποίο όλες οι πλευρές είναι ίσες ονομάζεται διαμάντι

Ιδιότητες ρόμβου:

1. Οι διαγώνιοι ενός ρόμβου είναι μεταξύ τους κάθετες και είναι οι διχοτόμοι των γωνιών του.

Απόδειξη

Αφήστε τις διαγώνιες $AC$ και $BD$ στον ρόμβο $ABCD$ να τέμνονται στο σημείο $O$. Εφόσον ένας ρόμβος είναι παραλληλόγραμμο, $AO=OC$. Θεωρήστε το ισοσκελές τρίγωνο $ABC$. Εφόσον το $AO$ είναι η διάμεσος που τραβιέται στη βάση, είναι η διχοτόμος και το ύψος, που απαιτούνται.

Σημάδια ενός διαμαντιού:

1. Αν οι διαγώνιοι ενός παραλληλογράμμου είναι αμοιβαία κάθετες, τότε αυτό το παραλληλόγραμμο είναι ρόμβος.
2. Αν η διαγώνιος ενός παραλληλογράμμου είναι η διχοτόμος της γωνίας του, τότε αυτό το παραλληλόγραμμο είναι ρόμβος.

Απόδειξη

Έστω ότι το παραλληλόγραμμο $ABCD$ έχει διαγώνιες $AC$ και $BD$ που τέμνονται στο σημείο $O$. Εξετάστε το τρίγωνο $ABC$.

1. Εάν οι διαγώνιοι είναι κάθετες, τότε το $BO$ είναι η διάμεσος και το ύψος του τριγώνου.

2. Εάν η διαγώνιος $BD$ περιέχει τη διχοτόμο της γωνίας $ABC$, τότε η $BO$ είναι η διάμεσος και η διχοτόμος στο τρίγωνο.

Και στις δύο περιπτώσεις, βρίσκουμε ότι το τρίγωνο $ABC$ είναι ισοσκελές και σε ένα παραλληλόγραμμο οι διπλανές πλευρές είναι ίσες. Επομένως, είναι ρόμβος, το οποίο ήταν και το ζητούμενο.

Ορισμός

Ένα ορθογώνιο του οποίου οι δύο γειτονικές πλευρές είναι ίσες ονομάζεται τετράγωνο.

Σημάδια τετραγώνου:

1. Αν ένας ρόμβος έχει ορθή γωνία, τότε αυτός ο ρόμβος είναι τετράγωνο.
2. Αν ένας ρόμβος έχει ίσες διαγώνιες, τότε ο ρόμβος είναι τετράγωνο.

Απόδειξη

Αν ένα παραλληλόγραμμο έχει ορθή γωνία ή ίσες διαγώνιους, τότε είναι ορθογώνιο. Αν ένα τετράπλευρο είναι ορθογώνιο και ρόμβος, τότε είναι τετράγωνο.