ในส่วนนี้ เราจะดูที่วัตถุทางเรขาคณิต สี่เหลี่ยมด้านขนาน องค์ประกอบทั้งหมดของสี่เหลี่ยมด้านขนานสืบทอดมาจากรูปสี่เหลี่ยมขนมเปียกปูน ดังนั้นเราจะไม่พิจารณาองค์ประกอบเหล่านั้น แต่คุณสมบัติและคุณลักษณะสมควรได้รับการพิจารณาอย่างละเอียด เราจะดูที่:
- ป้ายแตกต่างจากทรัพย์สินอย่างไร?
- มาดูคุณสมบัติและลักษณะพื้นฐานที่ศึกษาในหลักสูตรชั้นประถมศึกษาปีที่ 8 กัน
- ให้เรากำหนดคุณสมบัติเพิ่มเติมสองประการที่เราได้รับเมื่อแก้ไขปัญหาการสนับสนุน
2.1 คำจำกัดความของสี่เหลี่ยมด้านขนาน
ในการกำหนดแนวคิดทางเรขาคณิตอย่างถูกต้อง คุณไม่เพียงแต่ต้องจดจำแนวคิดเหล่านั้นเท่านั้น แต่ยังต้องเข้าใจว่าแนวคิดเหล่านั้นเกิดขึ้นได้อย่างไรอีกด้วย ในเรื่องนี้ โครงร่างของแนวคิดทั่วไปช่วยเราได้อย่างดี มาดูกันว่ามันคืออะไร
โมดูลการฝึกอบรมของเราเรียกว่า "รูปสี่เหลี่ยม" และรูปสี่เหลี่ยมขนมเปียกปูนเป็นแนวคิดหลักในหลักสูตรนี้ เราสามารถให้คำจำกัดความของรูปสี่เหลี่ยมขนมเปียกปูนได้ดังต่อไปนี้:
จัตุรัส-นี้ รูปหลายเหลี่ยมซึ่งมีสี่ด้านและสี่จุดยอด
ในคำจำกัดความนี้ แนวคิดทั่วไปจะเป็นรูปหลายเหลี่ยม ตอนนี้เรามากำหนดรูปหลายเหลี่ยมกัน:
รูปหลายเหลี่ยมเรียกว่าปิดง่าย เส้นขาดพร้อมกับส่วนของเครื่องบินที่มันบินไป
เห็นได้ชัดว่าแนวคิดทั่วไปในที่นี้คือแนวคิดเรื่องเส้นขาด หากเราไปไกลกว่านี้ เราจะมาถึงแนวคิดของเซ็กเมนต์ จากนั้นจึงมาถึงแนวคิดสุดท้ายของจุดและเส้นตรง ในทำนองเดียวกัน เราสามารถต่อแผนภาพของเราลงไปได้:
ถ้าเราต้องการให้ด้านสองด้านของรูปสี่เหลี่ยมขนมเปียกปูนขนานกันแต่สองด้านไม่ขนานกัน เราจะได้รูปทรงที่เรียกว่าสี่เหลี่ยมคางหมู
สี่เหลี่ยมคางหมู – รูปสี่เหลี่ยมโดยที่ด้านทั้งสองขนานกันและอีกสองด้านไม่ขนานกัน
และในกรณีที่ด้านตรงข้ามขนานกัน เรากำลังเผชิญกับสี่เหลี่ยมด้านขนาน
สี่เหลี่ยมด้านขนาน – รูปสี่เหลี่ยมซึ่งมีด้านตรงข้ามขนานกัน
2.2 คุณสมบัติของรูปสี่เหลี่ยมด้านขนาน
คุณสมบัติ 1.ในสี่เหลี่ยมด้านขนาน ด้านตรงข้ามจะเท่ากัน และมุมตรงข้ามจะเท่ากัน
 มาพิสูจน์คุณสมบัตินี้กัน
มาพิสูจน์คุณสมบัตินี้กัน
ที่ให้ไว้: ABCD เป็นสี่เหลี่ยมด้านขนาน
พิสูจน์:$\มุม A = \มุม C, \มุม B = \มุม D, AB = ซีดี, AD = BC.$
การพิสูจน์:
เมื่อพิสูจน์คุณสมบัติของวัตถุทางเรขาคณิตใดๆ เราจะจำคำจำกัดความของมันเสมอ ดังนั้น, สี่เหลี่ยมด้านขนาน- รูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกัน ประเด็นสำคัญที่นี่คือความขนานของด้านข้าง
เรามาสร้างเส้นตัดของเส้นทั้งสี่เส้นกัน เส้นตัดนี้จะเป็นเส้นทแยงมุม BD

แน่นอนว่าเราต้องพิจารณามุมที่เกิดจากเส้นตัดขวางและเส้นขนาน เนื่องจากเส้นตรงขนานกัน มุมที่วางขวางจึงเท่ากัน
ตอนนี้คุณสามารถเห็นสามเหลี่ยมสองรูปเท่ากันตามเครื่องหมายที่สอง
ความเท่าเทียมกันของรูปสามเหลี่ยมแสดงถึงคุณสมบัติแรกของรูปสี่เหลี่ยมด้านขนานโดยตรง
คุณสมบัติ 2.เส้นทแยงมุมของสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด

ที่ให้ไว้: เอบีซีดี- สี่เหลี่ยมด้านขนาน
พิสูจน์:$AO = OC, BO = OD.$
การพิสูจน์:
ตรรกะของการพิสูจน์ตรงนี้เหมือนกับคุณสมบัติก่อนหน้า นั่นคือ ความขนานของด้านและความเท่ากันของรูปสามเหลี่ยม ขั้นตอนแรกของการพิสูจน์จะเหมือนกับคุณสมบัติแรก
ขั้นตอนที่สองคือการพิสูจน์ความเท่าเทียมกันของรูปสามเหลี่ยมตามเกณฑ์ที่สอง โปรดทราบว่าสามารถยอมรับความเท่าเทียมกัน $BC=AD$ ได้โดยไม่ต้องพิสูจน์ (โดยใช้ คุณสมบัติ 1).
จากความเท่าเทียมกันนี้ จะได้ว่า $AO = OC, BO = OD.$

2.3 ปัญหารองรับข้อที่ 4 (คุณสมบัติของมุมระหว่างความสูงของรูปสี่เหลี่ยมด้านขนาน)

ที่ให้ไว้: เอบีซีดี - สี่เหลี่ยมด้านขนาน บี.เค. และ บี.เอ็ม. - ความสูงของมัน $\มุม KBM = 60^0$.
หา:$\มุม ABK$, $\มุม A$
สารละลาย:เมื่อเริ่มแก้ไขปัญหานี้ คุณต้องคำนึงถึงสิ่งต่อไปนี้:
ความสูงในรูปสี่เหลี่ยมด้านขนานตั้งฉากกับด้านตรงข้ามทั้งสอง
ตัวอย่างเช่น หากส่วน $BM$ ถูกลากไปที่ด้าน $DC$ และเป็นความสูง ($BM \perp DC$) ดังนั้นส่วนเดียวกันนี้จะเป็นความสูงไปทางด้านตรงข้าม ($BM \perp BA$) สิ่งนี้ตามมาจากความขนานของด้าน $AB \parallel DC$

เมื่อแก้ไขปัญหานี้ทรัพย์สินที่เราได้รับก็มีคุณค่า
ทรัพย์สินเพิ่มเติมมุมระหว่างความสูงของรูปสี่เหลี่ยมด้านขนานที่ดึงมาจากจุดยอดจะเท่ากับมุมที่จุดยอดที่อยู่ติดกัน
2.4 ปัญหารองรับข้อที่ 5 (คุณสมบัติของเส้นแบ่งครึ่งของสี่เหลี่ยมด้านขนาน)

เส้นแบ่งครึ่งมุม กสี่เหลี่ยมด้านขนาน เอบีซีดีข้ามด้านข้าง บี.ซี.ตรงจุด ล, ค.ศ.=12ซม, เอบี =10 ซม- ค้นหาความยาวของส่วน แอล.ซี..
สารละลาย:
- $\มุม 1 = \มุม 2$ (AK - เส้นแบ่งครึ่ง);
- $\angle 2 = \angle 3$ (เป็นมุมขวางที่มี $AD \parallel BC$ และเซคแคนต์ AL)
- $\angle 1 = \angle 3$, $\bigtriangleup ABL -$ หน้าจั่ว
ในระหว่างการแก้ปัญหา เราได้รับคุณสมบัติดังต่อไปนี้:
ทรัพย์สินเพิ่มเติมเส้นแบ่งครึ่งของมุมของสี่เหลี่ยมด้านขนานจะตัดสามเหลี่ยมหน้าจั่วออกไป
ในการพิจารณาว่ารูปที่กำหนดเป็นสี่เหลี่ยมด้านขนานหรือไม่นั้น จะต้องมีสัญญาณจำนวนหนึ่ง มาดูคุณสมบัติหลักสามประการของสี่เหลี่ยมด้านขนานกัน
เครื่องหมายสี่เหลี่ยมด้านขนาน 1 อัน
ถ้าด้านสองด้านของรูปสี่เหลี่ยมด้านขนานเท่ากันและขนานกัน รูปสี่เหลี่ยมด้านนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน
การพิสูจน์:
พิจารณารูปสี่เหลี่ยม ABCD ให้ด้าน AB และ CD ขนานกัน และให้ AB=CD ลองวาดเส้นทแยงมุม BD ลงไป มันจะแบ่งรูปสี่เหลี่ยมนี้ออกเป็นสามเหลี่ยมสองรูปเท่าๆ กัน: ABD และ CBD
สามเหลี่ยมเหล่านี้จะเท่ากันทั้งสองด้านและมีมุมระหว่างกัน (BD คือด้านร่วม, AB = CD โดยเงื่อนไข, มุม 1 = มุม 2 เป็นมุมขวางโดยมี BD ตัดขวางของเส้นคู่ขนาน AB และ CD) ดังนั้นมุม 3 = มุม 4
และมุมเหล่านี้จะนอนขวางเมื่อเส้น BC และ AD ตัดกับเส้นตัด BD จากนี้ไป BC และ AD ขนานกัน เรามีว่าในรูปสี่เหลี่ยม ABCD ด้านตรงข้ามขนานกันเป็นคู่ ดังนั้นรูปสี่เหลี่ยม ABCD จึงเป็นสี่เหลี่ยมด้านขนาน
เครื่องหมายสี่เหลี่ยมด้านขนานที่ 2
ถ้าในรูปสี่เหลี่ยมด้านขนานด้านตรงข้ามเท่ากันเป็นคู่ รูปสี่เหลี่ยมด้านขนานนี้จะเป็นสี่เหลี่ยมด้านขนาน
การพิสูจน์:
พิจารณารูปสี่เหลี่ยม ABCD ลองวาดเส้นทแยงมุม BD ลงไป มันจะแบ่งรูปสี่เหลี่ยมนี้ออกเป็นสามเหลี่ยมสองรูปเท่าๆ กัน: ABD และ CBD

สามเหลี่ยมทั้งสองนี้จะเท่ากันทั้งสามด้าน (BD คือด้านร่วม, AB = CD และ BC = AD ตามเงื่อนไข) จากนี้เราสามารถสรุปได้ว่ามุม 1 = มุม 2 ตามมาว่า AB ขนานกับ CD และเนื่องจาก AB = CD และ AB ขนานกับ CD ดังนั้นตามเกณฑ์แรกของรูปสี่เหลี่ยมด้านขนาน ABCD ของรูปสี่เหลี่ยมขนมเปียกปูนจึงเป็นรูปสี่เหลี่ยมด้านขนาน
3 เครื่องหมายสี่เหลี่ยมด้านขนาน
ถ้าเส้นทแยงมุมของรูปสี่เหลี่ยมตัดกันและถูกแบ่งครึ่งด้วยจุดตัด รูปสี่เหลี่ยมนี้จะเป็นสี่เหลี่ยมด้านขนาน
พิจารณารูปสี่เหลี่ยม ABCD ให้เราวาดเส้นทแยงมุม AC และ BD สองเส้นในนั้น ซึ่งจะตัดกันที่จุด O และถูกแบ่งออกเป็นสองส่วนโดยจุดนี้

สามเหลี่ยม AOB และ COD จะเท่ากันตามเครื่องหมายแรกของความเท่าเทียมกันของรูปสามเหลี่ยม (AO = OC, BO = OD โดยเงื่อนไข มุม AOB = มุม COD เป็นมุมแนวตั้ง) ดังนั้น AB = CD และมุม 1 = มุม 2 จากความเท่ากันของมุม 1 และ 2 เราจะได้ว่า AB ขนานกับ CD จากนั้นเราได้ว่าใน ABCD ของรูปสี่เหลี่ยมด้านขนาน ด้าน AB เท่ากับ CD และขนานกัน และตามเกณฑ์แรกของรูปสี่เหลี่ยมด้านขนาน ABCD ของรูปสี่เหลี่ยมด้านขนานจะเป็นรูปสี่เหลี่ยมด้านขนาน
คำนิยาม
สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกันเป็นคู่
รูปที่ 1 แสดงสี่เหลี่ยมด้านขนาน $A B C D, A B\|C D, B C\| เอ ดี$
คุณสมบัติของสี่เหลี่ยมด้านขนาน
- ในรูปสี่เหลี่ยมด้านขนาน ด้านตรงข้ามจะเท่ากัน: $A B=C D, B C=A D$ (รูปที่ 1)
- ในสี่เหลี่ยมด้านขนาน มุมตรงข้ามจะเท่ากับ $\angle A=\angle C, \angle B=\angle D$ (รูปที่ 1)
- เส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่จุดตัดแบ่งออกเป็นครึ่ง $A O=O C, B O=O D$ (รูปที่ 1)
- เส้นทแยงมุมของสี่เหลี่ยมด้านขนานแบ่งออกเป็นสามเหลี่ยมสองรูปเท่าๆ กัน
- ในสี่เหลี่ยมด้านขนาน มุมระหว่างระดับความสูงจะเท่ากับมุมแหลม: $\angle K B H=\angle A$
- เส้นแบ่งครึ่งของมุมที่อยู่ติดกับด้านหนึ่งของสี่เหลี่ยมด้านขนานจะตั้งฉากกัน
- เส้นแบ่งครึ่งของมุมตรงข้ามสองมุมของสี่เหลี่ยมด้านขนานจะขนานกัน
ผลรวมของมุมของสี่เหลี่ยมด้านขนานที่อยู่ติดกับด้านหนึ่งคือ $180^(\circ)$:
$$\มุม A+\มุม B=180^(\circ), \มุม B+\มุม C=180^(\circ)$$
$$\มุม C+\มุม D=180^(\circ), \มุม D+\มุม A=180^(\circ)$$
เส้นทแยงมุมและด้านข้างของสี่เหลี่ยมด้านขนานมีความสัมพันธ์กันโดยความสัมพันธ์ต่อไปนี้:
$$d_(1)^(2)+d_(2)^(2)=2 ก^(2)+2 ข^(2)$$
สัญญาณของรูปสี่เหลี่ยมด้านขนาน
รูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ เป็นสี่เหลี่ยมด้านขนานถ้า
- $A B=C D$ และ $A B \| ซี ดี$
- $A B=C D$ และ $B C=A D$
- $A O=O C$ และ $B O=O D$
- $\angle A=\มุม C$ และ $\angle B=\angle D$
พื้นที่ของสี่เหลี่ยมด้านขนานสามารถคำนวณได้โดยใช้สูตรใดสูตรหนึ่งต่อไปนี้:
$S=a \cdot h_(a), \quad S=b \cdot h_(b)$
$S=a \cdot b \cdot \sin \alpha, \quad S=\frac(1)(2) d_(1) \cdot d_(2) \cdot \sin \phi$
ตัวอย่างการแก้ปัญหา
ตัวอย่าง
ออกกำลังกาย.ผลรวมของสองมุมของสี่เหลี่ยมด้านขนานคือ $140^(\circ)$ หามุมที่ยิ่งใหญ่ที่สุดของสี่เหลี่ยมด้านขนาน
สารละลาย.ในสี่เหลี่ยมด้านขนาน มุมตรงข้ามจะเท่ากัน ลองแสดงว่ามุมที่ใหญ่กว่าของสี่เหลี่ยมด้านขนานเป็น $\alpha$ และมุมที่เล็กกว่าเป็น $\beta$ ผลรวมของมุม $\alpha$ และ $\beta$ คือ $180^(\circ)$ ดังนั้นผลรวมที่กำหนดเท่ากับ $140^(\circ)$ คือผลรวมของสองมุมที่ตรงกันข้ามกัน จากนั้น $140^(\circ) : 2=70 ^(\circ)$. ดังนั้นมุมที่เล็กกว่าคือ $\beta=70^(\circ)$ เราพบมุมที่ใหญ่กว่า $\alpha$ จากความสัมพันธ์:
$\alpha+\beta=180^(\circ) \ลูกศรขวา \alpha=180^(\circ)-\beta \ลูกศรขวา$
$\ลูกศรขวา \alpha=180^(\circ)-70^(\circ) \ลูกศรขวา \alpha=110^(\circ)$
คำตอบ.$\alpha=110^(\circ)$
ตัวอย่าง
ออกกำลังกาย.ด้านข้างของสี่เหลี่ยมด้านขนานคือ 18 ซม. และ 15 ซม. และความสูงที่ลากไปทางด้านที่สั้นกว่าคือ 6 ซม. จงหาความสูงอีกด้านหนึ่งของสี่เหลี่ยมด้านขนาน
สารละลาย.มาวาดรูปกันเถอะ (รูปที่ 2)

ตามเงื่อนไข $a=15$ cm, $b=18$ cm, $h_(a)=6$ cm สำหรับรูปสี่เหลี่ยมด้านขนาน สูตรต่อไปนี้ใช้ได้กับการค้นหาพื้นที่:
$$S=a \cdot h_(a), \quad S=b \cdot h_(b)$$
ให้เราถือด้านขวาของความเท่าเทียมกันเหล่านี้แล้วแสดง $h_(b) $: จากผลลัพธ์ที่เท่าเทียมกัน
$$a \cdot h_(a)=b \cdot h_(b) \ลูกศรขวา h_(b)=\frac(a \cdot h_(a))(b)$$
แทนที่ข้อมูลเบื้องต้นของปัญหา ในที่สุดเราก็ได้:
$h_(b)=\frac(15 \cdot 6)(18) \ลูกศรขวา h_(b)=5$ (ซม.)
แนวคิดเรื่องสี่เหลี่ยมด้านขนาน
คำจำกัดความ 1
สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกัน (รูปที่ 1)
รูปที่ 1.
สี่เหลี่ยมด้านขนานมีคุณสมบัติหลักสองประการ ลองพิจารณาโดยไม่มีข้อพิสูจน์
คุณสมบัติ 1: ด้านตรงข้ามและมุมของสี่เหลี่ยมด้านขนานจะเท่ากันตามลำดับ
คุณสมบัติ 2: เส้นทแยงมุมที่วาดในรูปสี่เหลี่ยมด้านขนานจะถูกแบ่งครึ่งตามจุดตัด
สัญญาณของรูปสี่เหลี่ยมด้านขนาน
ลองพิจารณาคุณลักษณะสามประการของสี่เหลี่ยมด้านขนานแล้วนำเสนอในรูปแบบของทฤษฎีบท
ทฤษฎีบท 1
หากด้านสองด้านของรูปสี่เหลี่ยมด้านขนานเท่ากันและขนานกัน รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน
การพิสูจน์.
ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AB||CD$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ในนั้น (รูปที่ 2)

รูปที่ 2.
พิจารณาเส้นคู่ขนาน $AB$ และ $CD$ และเส้นตัดกัน $AC$ แล้ว
\[\มุม CAB=\มุม DCA\]
เหมือนมุมที่ไขว้กัน
ตามเกณฑ์ $I$ ของความเท่าเทียมกันของรูปสามเหลี่ยม
เนื่องจาก $AC$ เป็นด้านร่วม และ $AB=CD$ ตามเงื่อนไข วิธี
\[\มุม DAC=\มุม ACB\]
พิจารณาเส้นตรง $AD$ และ $CB$ และเส้นตัดขวาง $AC$; จากความเท่ากันสุดท้ายของมุมนอน เราจะได้ $AD||CB$.) ดังนั้น ตามคำจำกัดความ $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน
ทฤษฎีบทได้รับการพิสูจน์แล้ว
ทฤษฎีบท 2
ถ้าด้านตรงข้ามของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากัน แสดงว่าเป็นรูปสี่เหลี่ยมด้านขนาน
การพิสูจน์.
ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ โดยที่ $AD=BC$ และ $AB=CD$ ให้เราวาดเส้นทแยงมุม $AC$ ไว้ข้างใน (รูปที่ 3)

รูปที่ 3.
เนื่องจาก $AD=BC$, $AB=CD$ และ $AC$ เป็นด้านร่วม ดังนั้นตามเกณฑ์ $III$ สำหรับความเท่ากันของรูปสามเหลี่ยม
\[\สามเหลี่ยม DAC=\สามเหลี่ยม ACB\]
\[\มุม DAC=\มุม ACB\]
ลองพิจารณาเส้น $AD$ และ $CB$ และเส้นตัดขวาง $AC$; ดังนั้น ตามคำนิยาม $1$ รูปสี่เหลี่ยมด้านขนานนี้จึงเป็นสี่เหลี่ยมด้านขนาน
\[\มุม DCA=\มุม CAB\]
ให้เราพิจารณาเส้น $AB$ และ $CD$ และเส้นตัดขวาง $AC$; จากความเท่าเทียมกันสุดท้ายในมุมโกหก เราจะได้ $AB||CD$ ดังนั้น ตามคำจำกัดความที่ 1 รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน
ทฤษฎีบทได้รับการพิสูจน์แล้ว
ทฤษฎีบท 3
หากเส้นทแยงมุมที่วาดเป็นรูปสี่เหลี่ยมขนมเปียกปูนถูกแบ่งออกเป็นสองส่วนเท่าๆ กันด้วยจุดตัดกัน รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน
การพิสูจน์.
ให้เราได้รับรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ ลองวาดเส้นทแยงมุม $AC$ และ $BD$ ลงไป ปล่อยให้พวกมันตัดกันที่จุด $O$ (รูปที่ 4)
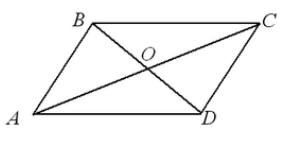
รูปที่ 4.
เนื่องจากตามเงื่อนไข $BO=OD,\ AO=OC$ และมุม $\angle COB=\angle DOA$ นั้นเป็นแนวตั้ง ดังนั้น ด้วยเกณฑ์ $I$ สำหรับความเท่าเทียมกันของรูปสามเหลี่ยม
\[\สามเหลี่ยม BOC=\สามเหลี่ยม AOD\]
\[\มุม DBC=\มุม BDA\]
พิจารณาเส้น $BC$ และ $AD$ และเส้นตัดขวาง $BD$; โดยความเสมอภาคสุดท้ายข้ามมุมโกหก เราจะได้ $BC||AD$ $BC=AD$ เช่นกัน ดังนั้น ตามทฤษฎีบท $1$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จึงเป็นสี่เหลี่ยมด้านขนาน
คำนิยาม
สี่เหลี่ยมด้านขนานคือรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกันเป็นคู่
เรียกว่าจุดตัดของเส้นทแยงมุมของสี่เหลี่ยมด้านขนาน ศูนย์.
คุณสมบัติของสี่เหลี่ยมด้านขนาน:
- ผลรวมของมุมสองมุมที่อยู่ติดกันของสี่เหลี่ยมด้านขนานคือ $180^(\circ)$ และมุมที่ตรงกันข้ามจะเท่ากัน
- ด้านตรงข้ามของสี่เหลี่ยมด้านขนานเท่ากัน
- เส้นทแยงมุมของสี่เหลี่ยมด้านขนานตัดและแบ่งครึ่งที่จุดตัดกัน
การพิสูจน์
ให้ $ABCD$ เป็นรูปสี่เหลี่ยมด้านขนาน
1. โปรดทราบว่ามุมที่อยู่ติดกัน $A$ และ $B$ ของสี่เหลี่ยมด้านขนานเป็นมุมภายในด้านเดียวที่มีเส้นขนาน $AD$ และ $BC$ และมีเส้นตัดมุม $AB$ นั่นคือ ผลรวมของมุมทั้งสองเท่ากับ $180^ \เซอร์กิต$. ในทำนองเดียวกันสำหรับมุมคู่อื่นๆ
ถ้า $\angle A + \angle B=180^\circ$ และ $\angle C + \angle B=180^\circ$ แล้ว $\angle A = \angle C$ ในทำนองเดียวกัน $\angle B = \angle D$
2. พิจารณารูปสามเหลี่ยม $ABC$ และ $CDA$ จากความขนานของด้านตรงข้ามของสี่เหลี่ยมด้านขนาน จะได้ว่า $\angle BAC=\angle DCA$ และ $\angle BCA=\angle DAC$ เนื่องจาก $AC$ เป็นเรื่องธรรมดา ดังนั้นรูปสามเหลี่ยม $ABC$ และ $CDA$ จึงเท่ากันตามเกณฑ์ที่สอง จากความเท่าเทียมกันของรูปสามเหลี่ยม จะได้ว่า $AB=CD$ และ $BC=AD$
3. เนื่องจากรูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนนูนออกมา เส้นทแยงมุมจึงตัดกัน ให้ $O$ เป็นจุดตัด จากความขนานของด้าน $BC$ และ $AD$ ของสี่เหลี่ยมด้านขนาน จะได้ว่า $\angle OAD=\angle OCB$ และ $\angle ODA=\angle OBC$ เมื่อคำนึงถึงความเท่าเทียมกัน $BC=AD$ เราจะได้สามเหลี่ยม $AOD$ และ $COB$ เท่ากันตามเกณฑ์ที่สอง ดังนั้น $AO=CO$ และ $DO=BO$ ตามที่ต้องการ

สัญญาณของรูปสี่เหลี่ยมด้านขนาน:
- หากในรูปสี่เหลี่ยมขนมเปียกปูนผลรวมของมุมสองมุมที่อยู่ติดกันคือ $180^(\circ)$ รูปสี่เหลี่ยมขนมเปียกปูนนี้จะเป็นรูปสี่เหลี่ยมด้านขนาน
- หากในรูปสี่เหลี่ยมขนมเปียกปูน มุมตรงข้ามเท่ากันเป็นคู่ รูปสี่เหลี่ยมขนมเปียกปูนนี้จะเป็นสี่เหลี่ยมด้านขนาน
- ถ้าในรูปสี่เหลี่ยมด้านขนานด้านตรงข้ามเท่ากันเป็นคู่ รูปสี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมด้านขนาน
- หากด้านสองด้านของรูปสี่เหลี่ยมขนมเปียกปูนเท่ากันและขนานกัน รูปสี่เหลี่ยมขนมเปียกปูนจะเป็นรูปสี่เหลี่ยมด้านขนาน
- หากเส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนถูกแบ่งครึ่งด้วยจุดตัด รูปสี่เหลี่ยมขนมเปียกปูนนั้นก็จะเป็นรูปสี่เหลี่ยมด้านขนาน
การพิสูจน์
ให้ $ABCD$ เป็นรูปสี่เหลี่ยม
1. โปรดทราบว่ามุมที่อยู่ติดกัน $A$ และ $B$ เป็นมุมภายในด้านเดียวที่มีเส้นตรง $AD$ และ $BC$ และมีเส้นตัดขวาง $AB$ เนื่องจากผลรวมของพวกเขาคือ $180^\circ$ ดังนั้นเส้น $AD$ และ $BC$ จึงขนานกัน ในทำนองเดียวกันสำหรับเส้นอีกคู่หนึ่ง นั่นคือ $ABCD$ เป็นสี่เหลี่ยมด้านขนานตามคำจำกัดความ
2. โปรดทราบว่า $\angle A + \angle B + \angle C + \angle D=360^\circ$ ถ้า $\angle A = \angle C$ และ $\angle B = \angle D$ แล้ว $\angle A + \angle B=180^\circ$ และในทำนองเดียวกันสำหรับคู่อื่นๆ ของมุมที่อยู่ติดกัน ต่อไปเราใช้เครื่องหมายก่อนหน้า
3. พิจารณารูปสามเหลี่ยม $ABC$ และ $CDA$ เนื่องจาก $AC$ เป็นเรื่องธรรมดา ดังนั้น จากความเท่ากันของด้านตรงข้ามของสี่เหลี่ยมด้านขนาน สามเหลี่ยม $ABC$ และ $CDA$ จะเท่ากันตามเกณฑ์ที่สาม ดังนั้น $\angle BAC=\angle DCA$ และ $\angle BCA=\angle DAC$ ซึ่งแสดงถึงความขนานของด้านตรงข้าม
4. ให้ $BC$ และ $AD$ เท่ากันและขนานกัน พิจารณารูปสามเหลี่ยม $ABC$ และ $CDA$ จากความขนานของเส้นตรง จะได้ว่า $\angle BCA=\angle DAC$ เนื่องจาก $AC$ เป็นค่าทั่วไปและ $BC=AD$ ดังนั้นสามเหลี่ยม $ABC$ และ $CDA$ จะเท่ากันตามเกณฑ์แรก ดังนั้น $AB=CD$ ต่อไปเราใช้เครื่องหมายก่อนหน้า
5. ให้ $O$ เป็นจุดตัดของเส้นทแยงมุมกับ $AO=CO$ และ $DO=BO$ เมื่อคำนึงถึงความเท่าเทียมกันของมุมแนวตั้ง เราจะได้สามเหลี่ยม $AOD$ และ $COB$ เท่ากันตามเกณฑ์แรก ดังนั้น $\angle OAD=\angle OCB$ ซึ่งแสดงถึงความขนานของ $BC$ และ $AD$ ในทำนองเดียวกันสำหรับอีกคู่หนึ่ง
คำนิยาม
รูปสี่เหลี่ยมที่มีสามมุมฉากเรียกว่า สี่เหลี่ยมผืนผ้า.
คุณสมบัติสี่เหลี่ยมผืนผ้า:
- เส้นทแยงมุมของสี่เหลี่ยมจะเท่ากัน
การพิสูจน์
ให้ $ABCD$ เป็นรูปสี่เหลี่ยมผืนผ้า เนื่องจากสี่เหลี่ยมผืนผ้าเป็นรูปสี่เหลี่ยมด้านขนาน ด้านตรงข้ามจึงเท่ากัน จากนั้นสามเหลี่ยมมุมฉาก $ABD$ และ $DCA$ จะเท่ากันทั้งสองขา ซึ่งหมายความว่า $BD=AC$
คุณสมบัติของสี่เหลี่ยมผืนผ้า:
- ถ้าสี่เหลี่ยมด้านขนานมีมุมฉาก สี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมผืนผ้า
- ถ้าเส้นทแยงมุมของสี่เหลี่ยมด้านขนานเท่ากัน สี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมผืนผ้า
การพิสูจน์
1. ถ้ามุมหนึ่งของรูปสี่เหลี่ยมด้านขนานเป็นเส้นตรง เมื่อพิจารณาว่าผลรวมของมุมที่อยู่ติดกันคือ $180^(\circ)$ เราก็จะได้ว่ามุมที่เหลือก็เป็นเส้นตรงเช่นกัน
2. ให้เส้นทแยงมุม $AC$ และ $BD$ เท่ากันในสี่เหลี่ยมด้านขนาน $ABCD$ เมื่อคำนึงถึงความเท่าเทียมกันของด้านตรงข้าม $AB$ และ $DC$ เราพบว่าสามเหลี่ยม $ABD$ และ $DCA$ เท่ากันตามเกณฑ์ที่สาม ดังนั้น $\angle BAD=\angle CDA$ นั่นคือ พวกมันเป็นเส้นตรง ยังคงใช้เครื่องหมายก่อนหน้า
คำนิยาม
เรียกว่ารูปสี่เหลี่ยมที่มีด้านเท่ากันทุกด้าน เพชร
คุณสมบัติของรูปสี่เหลี่ยมขนมเปียกปูน:
- เส้นทแยงมุมของสี่เหลี่ยมขนมเปียกปูนตั้งฉากกันและเป็นเส้นแบ่งครึ่งของมุมของมัน
การพิสูจน์
ให้เส้นทแยงมุม $AC$ และ $BD$ ในรูปสี่เหลี่ยมขนมเปียกปูน $ABCD$ ตัดกันที่จุด $O$ เนื่องจากสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมด้านขนาน $AO=OC$ พิจารณาสามเหลี่ยมหน้าจั่ว $ABC$ เนื่องจาก $AO$ คือค่ามัธยฐานที่ลากไปที่ฐาน มันคือเส้นแบ่งครึ่งและความสูง ซึ่งเป็นค่าที่ต้องการ
สัญญาณของเพชร:
- ถ้าเส้นทแยงมุมของสี่เหลี่ยมด้านขนานตั้งฉากกัน สี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมขนมเปียกปูน
- ถ้าเส้นทแยงมุมของสี่เหลี่ยมด้านขนานเป็นเส้นแบ่งครึ่งของมุม สี่เหลี่ยมด้านขนานนี้ก็จะเป็นรูปสี่เหลี่ยมขนมเปียกปูน
การพิสูจน์
ให้สี่เหลี่ยมด้านขนาน $ABCD$ มีเส้นทแยงมุม $AC$ และ $BD$ ตัดกันที่จุด $O$ พิจารณาสามเหลี่ยม $ABC$
1. ถ้าเส้นทแยงมุมตั้งฉากกัน $BO$ คือค่ามัธยฐานและความสูงของรูปสามเหลี่ยม
2. ถ้าเส้นทแยงมุม $BD$ มีเส้นแบ่งครึ่งของมุม $ABC$ แล้ว $BO$ จะเป็นค่ามัธยฐานและเป็นเส้นแบ่งครึ่งในรูปสามเหลี่ยม
ในทั้งสองกรณี เราพบว่าสามเหลี่ยม $ABC$ เป็นหน้าจั่ว และในรูปสี่เหลี่ยมด้านขนานด้านประชิดจะเท่ากัน ดังนั้นจึงเป็นรูปสี่เหลี่ยมขนมเปียกปูนซึ่งเป็นสิ่งที่จำเป็น
คำนิยาม
สี่เหลี่ยมที่มีด้านประชิดกันสองด้านเท่ากันเรียกว่า สี่เหลี่ยม.
สัญญาณของสี่เหลี่ยมจัตุรัส:
- ถ้าสี่เหลี่ยมขนมเปียกปูนมีมุมฉาก แล้วสี่เหลี่ยมขนมเปียกปูนนั้นก็เป็นรูปสี่เหลี่ยมจัตุรัส
- ถ้าสี่เหลี่ยมขนมเปียกปูนมีเส้นทแยงมุมเท่ากัน แสดงว่าสี่เหลี่ยมขนมเปียกปูนนั้นเป็นสี่เหลี่ยมจัตุรัส
การพิสูจน์
ถ้ารูปสี่เหลี่ยมด้านขนานมีมุมฉากหรือเส้นทแยงมุมเท่ากัน แสดงว่าเป็นสี่เหลี่ยมมุมฉาก ถ้ารูปสี่เหลี่ยมเป็นรูปสี่เหลี่ยมผืนผ้าและเป็นสี่เหลี่ยมขนมเปียกปูน แสดงว่าเป็นรูปสี่เหลี่ยมจัตุรัส











อาการของโรคระบบทางเดินปัสสาวะในผู้ชาย
วิธีรับประทานเมื่อถูกพิษ
คอมเพล็กซ์การออกกำลังกายตอนเช้าสำหรับเด็กของกลุ่มน้องที่สอง
เสียงในคำและประโยค
คำจำกัดความของมนุษย์ในฐานะสัตว์ทางการเมืองถูกกำหนดโดยอริสโตเติล ซึ่งเรียกมนุษย์ว่าเป็นสัตว์ทางการเมือง