صيغة الهرم الثلاثي. هرم. موارد الإنترنت

مفهوم الهرم

التعريف 1

يسمى الشكل الهندسي الذي يتكون من مضلع ونقطة غير موجودة في المستوى الذي يحتوي على هذا المضلع، والمتصل بجميع رؤوس المضلع، بالهرم (الشكل 1).

المضلع الذي يتكون منه الهرم يسمى قاعدة الهرم، والمثلثات الناتجة عند اتصالها بنقطة هي الأوجه الجانبية للهرم، وأضلاع المثلثات هي أضلاع الهرم، والنقطة المشتركة لجميع المثلثات هي قمة الهرم.

أنواع الأهرامات

اعتمادا على عدد الزوايا في قاعدة الهرم، يمكن أن يطلق عليه الثلاثي، الرباعي، وما إلى ذلك (الشكل 2).

الشكل 2.

نوع آخر من الهرم هو الهرم العادي.

دعونا نقدم ونثبت خاصية الهرم المنتظم.

النظرية 1

جميع الوجوه الجانبية للهرم المنتظم هي مثلثات متساوية الساقين ومتساوية فيما بينها.

دليل.

خذ بعين الاعتبار هرمًا منتظمًا $n-$gonal مع قمة $S$ للارتفاع $h=SO$. دعونا نرسم دائرة حول القاعدة (الشكل 4).

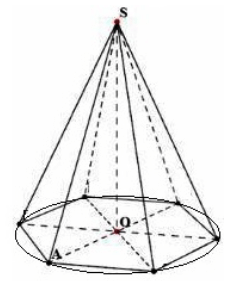
الشكل 4.

خذ بعين الاعتبار المثلث $SOA$. وفقا لنظرية فيثاغورس، نحصل على

من الواضح أنه سيتم تعريف أي حافة جانبية بهذه الطريقة. وبالتالي فإن جميع الحواف الجانبية متساوية مع بعضها البعض، أي أن جميع الوجوه الجانبية هي مثلثات متساوية الساقين. دعونا نثبت أنهم متساوون مع بعضهم البعض. وبما أن القاعدة مضلع منتظم، فإن قواعد جميع الوجوه الجانبية متساوية مع بعضها البعض. وبالتالي، فإن جميع الوجوه الجانبية متساوية وفقًا للمعيار الثالث لمساواة المثلثات.

لقد تم إثبات النظرية.

دعونا الآن نقدم التعريف التالي المتعلق بمفهوم الهرم المنتظم.

التعريف 3

قياس الهرم المنتظم هو ارتفاع وجهه الجانبي.

من الواضح، وفقًا للنظرية الأولى، أن جميع القياسات متساوية مع بعضها البعض.

النظرية 2

يتم تحديد مساحة السطح الجانبية للهرم العادي على أنها حاصل ضرب نصف محيط القاعدة والارتفاع.

دليل.

دعونا نشير إلى جانب قاعدة الهرم $n-$gonal بـ $a$، والارتفاع بـ $d$. وبالتالي فإن مساحة الوجه الجانبي تساوي

وبما أنه وفقًا للنظرية 1، فإن جميع الجوانب متساوية

لقد تم إثبات النظرية.

نوع آخر من الهرم هو الهرم المقطوع.

التعريف 4

إذا تم رسم مستوى موازٍ لقاعدته من خلال هرم عادي، فإن الشكل المتكون بين هذا المستوى ومستوى القاعدة يسمى الهرم المقطوع (الشكل 5).

الشكل 5. الهرم المقطوع

الوجوه الجانبية للهرم المقطوع هي شبه منحرف.

النظرية 3

يتم تحديد المساحة السطحية الجانبية للهرم المقطوع المنتظم على أنها حاصل ضرب مجموع أنصاف محيطات القواعد والارتفاع.

دليل.

دعونا نشير إلى جوانب قاعدتي الهرم $n-$gonal بـ $a\ و\b$، على التوالي، والارتفاع بـ $d$. وبالتالي فإن مساحة الوجه الجانبي تساوي

وبما أن جميع الأطراف متساوية، إذن

لقد تم إثبات النظرية.

مهمة عينة

مثال 1

أوجد مساحة السطح الجانبي للهرم الثلاثي المقطوع إذا تم الحصول عليه من هرم منتظم قاعدته 4 وعظمته 5 عن طريق قطع مستوى يمر عبر خط الوسط للأوجه الجانبية.

حل.

وباستخدام نظرية خط المنتصف نجد أن القاعدة العليا للهرم المقطوع تساوي $4\cdot \frac(1)(2)=2$، والقياس يساوي $5\cdot \frac(1)(2) =2.5$.

ثم، من خلال النظرية 3، نحصل على

تعريف

هرمهو متعدد السطوح يتكون من مضلع \(A_1A_2...A_n\) و\(n\) مثلثات ذات قمة مشتركة \(P\) (لا تقع في مستوى المضلع) وأضلاع مقابلة لها، تتزامن مع جوانب المضلع.
التعيين: \(PA_1A_2...A_n\) .
مثال: الهرم الخماسي \(PA_1A_2A_3A_4A_5\) .

المثلثات \(PA_1A_2، \PA_2A_3\)، إلخ. وتسمى وجوه جانبيةالأهرامات، والقطاعات \(PA_1، PA_2\)، وما إلى ذلك. - الأضلاع الجانبية, المضلع \(A_1A_2A_3A_4A_5\) – أساس، النقطة \(P\) – قمة.

ارتفاعالأهرامات هي خط عمودي ينحدر من أعلى الهرم إلى مستوى القاعدة.

يسمى الهرم الذي في قاعدته مثلث رباعي الاسطح.

الهرم يسمى صحيحإذا كانت قاعدته مضلعًا منتظمًا وتوافر أحد الشروط التالية:

\((أ)\) الحواف الجانبية للهرم متساوية؛

\((ب)\) يمر ارتفاع الهرم بمركز الدائرة المحددة بالقرب من القاعدة؛

\((ج)\) تميل الأضلاع الجانبية إلى مستوى القاعدة بنفس الزاوية.

\((د)\) تميل الوجوه الجانبية إلى مستوى القاعدة بنفس الزاوية.

رباعي الاسطح منتظمهو هرم ثلاثي، جميع وجوهه مثلثات متساوية الأضلاع.

نظرية

الشروط \((أ)، (ب)، (ج)، (د)\) متكافئة.

دليل

دعونا نجد ارتفاع الهرم \(PH\) . اجعل \(\alpha\) هو مستوى قاعدة الهرم.

1) لنثبت أن من \((a)\) يتبع \((b)\) . دع \(PA_1=PA_2=PA_3=...=PA_n\) .

لأن \(PH\perp \alpha\)، إذن \(PH\) متعامد على أي خط يقع في هذا المستوى، مما يعني أن المثلثات قائمة الزاوية. هذا يعني أن هذين المثلثين متساويان في الساق المشتركة \(PH\) والوتر \(PA_1=PA_2=PA_3=...=PA_n\) . هذا يعني \(A_1H=A_2H=...=A_nH\) . هذا يعني أن النقاط \(A_1, A_2, ..., A_n\) تقع على نفس المسافة من النقطة \(H\)، وبالتالي فهي تقع على نفس الدائرة التي يبلغ نصف قطرها \(A_1H\) . هذه الدائرة، بحكم تعريفها، محصورة حول المضلع \(A_1A_2...A_n\) .

2) دعونا نثبت أن \((b)\) يعني \((c)\) .

\(PA_1H، PA_2H، PA_3H،...، PA_nH\)مستطيلة ومتساوية على قدمين. وهذا يعني أن زواياهم متساوية أيضًا، وبالتالي، \(\الزاوية PA_1H=\الزاوية PA_2H=...=\الزاوية PA_nH\).

3) دعونا نثبت أن \((ج)\) تتضمن \((a)\) .

على غرار النقطة الأولى، المثلثات \(PA_1H، PA_2H، PA_3H،...، PA_nH\)مستطيلة على طول الساق والزاوية الحادة. وهذا يعني أن الوترين متساويان أيضًا، أي \(PA_1=PA_2=PA_3=...=PA_n\) .

4) دعونا نثبت أن \((b)\) يعني \((d)\) .

لأن في المضلع المنتظم، تتطابق مراكز الدوائر المقيدة والدوائر المنقوشة (بشكل عام، تسمى هذه النقطة مركز المضلع المنتظم)، ثم \(H\) هو مركز الدائرة المنقوشة. لنرسم خطوطًا متعامدة من النقطة \(H\) إلى جوانب القاعدة: \(HK_1, HK_2\)، إلخ. هذه هي أنصاف أقطار الدائرة المنقوشة (حسب التعريف). بعد ذلك، وفقًا لـ TTP (\(PH\) عمودي على المستوى، \(HK_1, HK_2\)، وما إلى ذلك هي إسقاطات متعامدة على الجوانب) مائلة \(PK_1, PK_2\)، إلخ. عمودي على الجوانب \(A_1A_2, A_2A_3\)، إلخ. على التوالى. لذلك، بحكم التعريف \(\الزاوية PK_1H، \الزاوية PK_2H\)مساوية للزوايا المحصورة بين الأوجه الجانبية والقاعدة. لأن المثلثات \(PK_1H, PK_2H, ...\) متساوية (كمستطيل من الجانبين)، ثم الزوايا \(\الزاوية PK_1H، \الزاوية PK_2H، ...\)متساوون.

5) دعونا نثبت أن \((د)\) تعني \((ب)\) .

على غرار النقطة الرابعة، المثلثات \(PK_1H, PK_2H, ...\) متساوية (كمستطيل على طول الساق والزاوية الحادة)، مما يعني أن القطع \(HK_1=HK_2=...=HK_n\) متساوية متساوي. وهذا يعني، بحكم التعريف، \(H\) هو مركز الدائرة المنقوشة في القاعدة. ولكن بالنسبة للمضلعات المنتظمة، يتطابق مركزا الدائرة المحصورة مع الدائرة المحصورة، فيكون \(H\) مركز الدائرة المحصورة. تشتد.

عاقبة

الوجوه الجانبية للهرم المنتظم هي مثلثات متساوية الساقين.

تعريف

يسمى ارتفاع الوجه الجانبي للهرم المنتظم المرسوم من رأسه apothem.
إن قياسات جميع الوجوه الجانبية للهرم المنتظم متساوية مع بعضها البعض وهي أيضًا متوسطات ومنصفات.

ملاحظات هامة

1. يقع ارتفاع الهرم الثلاثي المنتظم عند نقطة تقاطع ارتفاعات (أو منصفات، أو متوسطات) القاعدة (القاعدة مثلث منتظم).

2. يقع ارتفاع الهرم الرباعي المنتظم عند نقطة تقاطع قطري القاعدة (القاعدة مربعة).

3. يقع ارتفاع الهرم السداسي المنتظم عند نقطة تقاطع أقطار القاعدة (القاعدة مسدس منتظم).

4. يكون ارتفاع الهرم متعامدا مع أي خط مستقيم يقع عند القاعدة.

تعريف

الهرم يسمى مستطيليإذا كان أحد حوافها الجانبية متعامدًا مع مستوى القاعدة.

ملاحظات هامة

1. في الهرم المستطيل، تكون الحافة المتعامدة مع القاعدة هي ارتفاع الهرم. أي أن \(SR\) هو الارتفاع.

2. لأن \(SR\) عمودي على أي خط من القاعدة، إذن \(\مثلث SRM، \مثلث SRP\)- المثلثات القائمة.

3. المثلثات \(\مثلث SRN، \مثلث SRK\)- مستطيلة أيضًا.
أي أن أي مثلث يتكون من هذه الحافة والقطر الخارج من رأس هذه الحافة الواقع عند القاعدة يكون مستطيلاً.

\[(\Large(\text(حجم الهرم ومساحة سطحه))))\]

نظرية

حجم الهرم يساوي ثلث حاصل ضرب مساحة القاعدة وارتفاع الهرم: \

عواقب

اجعل \(a\) هو جانب القاعدة، \(h\) هو ارتفاع الهرم.

1. حجم الهرم الثلاثي المنتظم هو \(V_(\text(right Triangle.pir.))=\dfrac(\sqrt3)(12)a^2h\),

2. حجم الهرم الرباعي المنتظم هو \(V_(\text(right.four.pir.))=\dfrac13a^2h\).

3. حجم الهرم السداسي المنتظم هو \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).

4. حجم رباعي السطوح المنتظم هو \(V_(\text(tetr.))=\dfrac(\sqrt3)(12)a^3\).

نظرية

مساحة السطح الجانبي للهرم العادي تساوي نصف منتج محيط القاعدة والارتفاع.

\[(\كبير(\نص(فروستوم)))\]

تعريف

فكر في هرم عشوائي \(PA_1A_2A_3...A_n\) . دعونا نرسم مستوى موازيًا لقاعدة الهرم من خلال نقطة معينة تقع على الحافة الجانبية للهرم. هذا المستوى سيقسم الهرم إلى متعددات وجوه، أحدهما هرم ((\(PB_1B_2...B_n\)) والآخر يسمى الهرم المقطوع(\(A_1A_2...A_nB_1B_2...B_n\) ).

يحتوي الهرم المقطوع على قاعدتين - المضلعات \(A_1A_2...A_n\) و \(B_1B_2...B_n\) المتشابهة مع بعضها البعض.

ارتفاع الهرم المقطوع هو خط عمودي مرسوم من نقطة معينة من القاعدة العليا إلى مستوى القاعدة السفلية.

ملاحظات هامة

1. جميع الوجوه الجانبية للهرم المقطوع هي شبه منحرف.

2. الجزء الذي يربط بين مراكز قواعد الهرم المنتظم المقطوع (أي الهرم الناتج عن المقطع العرضي للهرم العادي) هو الارتفاع.

عندما يسمع الإنسان كلمة "الهرم" يتذكر على الفور الهياكل المصرية المهيبة. ومع ذلك، فإن العمالقة الحجرية القديمة ليست سوى واحدة من ممثلي فئة الهرم. في هذه المقالة سوف ننظر من وجهة نظر هندسية في خصائص الهرم الرباعي المنتظم.

ما هو الهرم بشكل عام؟

في الهندسة، يُفهم على أنه شكل ثلاثي الأبعاد، يمكن الحصول عليه من خلال ربط جميع رؤوس المضلع المسطح بنقطة واحدة تقع في مستوى مختلف عن هذا المضلع. ويوضح الشكل أدناه 4 أشكال تنطبق عليها هذا التعريف.

نلاحظ أن الشكل الأول له قاعدة مثلثة، والثاني له قاعدة رباعية الزوايا. يتم تمثيل الأخيرين بقاعدة خماسية وسداسية. ومع ذلك، فإن السطح الجانبي لجميع الأهرامات يتكون من مثلثات. عددهم يساوي تمامًا عدد أضلاع أو رؤوس المضلع عند القاعدة.

هناك نوع خاص من الهرم، والذي يختلف عن غيره من ممثلي الفصل في تماثله المثالي، هو الهرم العادي. لكي يكون الشكل صحيحاً، يجب استيفاء الشرطين التاليين:

• يجب أن يكون للقاعدة مضلع منتظم؛
• يجب أن يتكون السطح الجانبي للشكل من مثلثات متساوية الساقين.

لاحظ أنه يمكن استبدال الشرط الإلزامي الثاني بآخر وهو أن العمود المرسوم على القاعدة من أعلى الهرم (نقطة تقاطع المثلثات الجانبية) يجب أن يتقاطع مع هذه القاعدة عند مركزها الهندسي.

الآن دعنا ننتقل إلى موضوع المقال ونفكر في خصائص الهرم الرباعي المنتظم الذي يميزه. أولاً، دعونا نوضح في الشكل كيف يبدو هذا الشكل.

قاعدتها مربعة. تمثل الجوانب 4 مثلثات متساوية الساقين متطابقة (يمكن أيضًا أن تكون متساوية الأضلاع بنسبة معينة من طول جانب المربع وارتفاع الشكل). الارتفاع المخفض من أعلى الهرم سوف يتقاطع مع المربع في مركزه (نقطة تقاطع الأقطار).

يحتوي هذا الهرم على 5 وجوه (مربع وأربعة مثلثات)، و5 رؤوس (أربعة منها تنتمي إلى القاعدة) و8 حواف. الترتيب الرابع، الذي يمر عبر ارتفاع الهرم، يحوله إلى نفسه عن طريق الدوران 90 درجة.

الأهرامات المصرية بالجيزة مستطيلة الشكل ومنتظمة.

أربعة معلمات خطية أساسية

لنبدأ بدراسة الخصائص الرياضية للهرم الرباعي المنتظم باستخدام صيغ الارتفاع وطول ضلع القاعدة والحافة الجانبية والقياس. لنفترض على الفور أن كل هذه الكميات مرتبطة ببعضها البعض، لذا يكفي معرفة اثنتين منها فقط لحساب الكميتين المتبقيتين بشكل لا لبس فيه.

لنفترض أن ارتفاع h للهرم وطول a لضلع القاعدة المربعة معروفان، فإن الحافة الجانبية b ستساوي:

ب = √(أ 2 / 2 + ح 2)

الآن نعطي صيغة الطول a b للقياس (ارتفاع المثلث الذي ينخفض ​​إلى جانب القاعدة):

أ ب = √(أ ٢ / ٤ + ح ٢)

من الواضح أن الحافة الجانبية b تكون دائمًا أكبر من apothem a b .

يمكن استخدام كلا التعبيرين لتحديد جميع الخصائص الخطية الأربعة إذا كانت المعلمتان الأخريان معروفتين، على سبيل المثال a b وh.

مساحة وحجم الشكل

هاتان خاصيتان أكثر أهمية للهرم الرباعي المنتظم. تحتوي قاعدة الشكل على المساحة التالية:

كل تلميذ يعرف هذه الصيغة. يمكن تحديد مساحة السطح الجانبي الذي يتكون من أربعة مثلثات متطابقة من خلال الارتفاع أ ب للهرم كما يلي:

إذا كان a b غير معروف، فيمكن تحديده باستخدام الصيغ من الفقرة السابقة من خلال الارتفاع h أو الحافة b.

المساحة الإجمالية للشكل قيد النظر هي مجموع المساحات S o و S b:

S = S o + S b = أ 2 + 2 × أ × أ ب = أ (أ + 2 × أ ب)

المساحة المحسوبة لجميع وجوه الهرم موضحة في الشكل أدناه في شكل تطوره.

لن يكتمل وصف خصائص الهرم الرباعي المنتظم دون النظر في صيغة تحديد حجمه. يتم حساب قيمة الهرم المعني على النحو التالي:

أي أن V يساوي الجزء الثالث من حاصل ضرب ارتفاع الشكل ومساحة قاعدته.

خصائص الهرم الرباعي المنتظم

يمكنك الحصول على هذا الرقم من الهرم الأصلي. للقيام بذلك، تحتاج إلى قطع الجزء العلوي من الهرم بالطائرة. سيتم تسمية الشكل المتبقي تحت المستوى المقطوع بالهرم المقطوع.

من الأنسب دراسة خصائص الهرم المقطوع إذا كانت قواعده متوازية مع بعضها البعض. في هذه الحالة، ستكون القواعد السفلية والعلوية مضلعات متشابهة. نظرًا لأن القاعدة في الهرم المنتظم رباعي الزوايا عبارة عن مربع، فإن القسم المتكون أثناء القطع سيمثل أيضًا مربعًا، ولكن بحجم أصغر.

لا يتكون السطح الجانبي للشكل المقطوع من مثلثات، بل من شبه منحرف متساوي الساقين.

ومن الخصائص المهمة لهذا الهرم هو حجمه، والذي يتم حسابه بالصيغة:

V = 1/3 × ح × (S o1 + S o2 + √(S o1 × S o2))

هنا h هي المسافة بين قاعدتي الشكل، S o1، S o2 هي مساحات القاعدتين السفلية والعلوية.

الهرم هو متعدد السطوح مع مضلع في قاعدته. تشكل جميع الوجوه بدورها مثلثات تتقارب في قمة واحدة. الأهرامات مثلثة، ورباعية الزوايا، وهكذا. من أجل تحديد الهرم الذي أمامك، يكفي حساب عدد الزوايا عند قاعدته. غالبًا ما يتم العثور على تعريف "ارتفاع الهرم" في المشكلات الهندسية في المناهج المدرسية. سنحاول في هذه المقالة إلقاء نظرة على طرق مختلفة للعثور عليه.

أجزاء الهرم

ويتكون كل هرم من العناصر التالية:

• الوجوه الجانبية، التي لها ثلاث زوايا وتتقارب عند القمة؛
• يمثل الارتفاع الارتفاع الذي ينحدر من قمته.
• قمة الهرم هي النقطة التي تربط بين الأضلاع الجانبية ولكنها لا تقع في مستوى القاعدة.
• القاعدة عبارة عن مضلع لا يقع عليه الرأس؛
• ارتفاع الهرم هو الجزء الذي يتقاطع مع قمة الهرم ويشكل زاوية قائمة مع قاعدته.

كيفية العثور على ارتفاع الهرم إذا كان حجمه معروفا

من خلال الصيغة V = (S*h)/3 (في الصيغة V هو الحجم، S هي مساحة القاعدة، h هو ارتفاع الهرم) نجد أن h = (3*V)/ س. لتوحيد المواد، دعونا نحل المشكلة على الفور. حجم القاعدة المثلثة 50 سم2 وحجمها 125 سم3. ارتفاع الهرم الثلاثي غير معروف، وهو ما نحتاج إلى إيجاده. كل شيء بسيط هنا: نقوم بإدخال البيانات في صيغتنا. نحصل على ح = (3*125)/50 = 7.5 سم.

كيفية العثور على ارتفاع الهرم إذا كان طول القطر وحوافه معروفا

وكما نتذكر، فإن ارتفاع الهرم يشكل زاوية قائمة مع قاعدته. هذا يعني أن الارتفاع والحافة ونصف القطر معًا يشكلان الكثير، بالطبع، تذكروا نظرية فيثاغورس. وبمعرفة بعدين، لن يكون من الصعب إيجاد الكمية الثالثة. دعونا نتذكر النظرية المعروفة a² = b² + c²، حيث a هو الوتر، وفي حالتنا حافة الهرم؛ ب - الرجل الأولى أو نصف القطر و ج - على التوالي الرجل الثانية أو ارتفاع الهرم. من هذه الصيغة ج² = أ² - ب².

المشكلة الآن: في الهرم العادي يكون القطر 20 سم، عندما يكون طول الحافة 30 سم، عليك إيجاد الارتفاع. نحل: c² = 30² - 20² = 900-400 = 500. وبالتالي، c = √ 500 = حوالي 22.4.

كيفية العثور على ارتفاع الهرم المقطوع

وهو مضلع ذو مقطع عرضي موازي لقاعدته. ارتفاع الهرم المقطوع هو القطعة التي تصل بين قاعدتيه. يمكن معرفة الارتفاع للهرم المنتظم إذا كانت أطوال أقطار القاعدتين معروفة وكذلك حافة الهرم. اجعل قطر القاعدة الأكبر هو d1، بينما قطر القاعدة الأصغر هو d2، وطول الحافة l. للعثور على الارتفاع، يمكنك خفض الارتفاعات من النقطتين العلويتين المتقابلتين للمخطط إلى قاعدته. نلاحظ أن لدينا مثلثين قائمي الزاوية، وكل ما تبقى هو إيجاد أطوال أرجلهما. للقيام بذلك، اطرح الأصغر من القطر الأكبر واقسمه على 2. لذلك سنجد ساقًا واحدة: أ = (d1-d2)/2. وبعد ذلك، وفقًا لنظرية فيثاغورس، كل ما علينا فعله هو إيجاد الساق الثانية، وهي ارتفاع الهرم.

الآن دعونا نلقي نظرة على هذا الأمر برمته في الممارسة العملية. لدينا مهمة أمامنا. هرم مقطوع له مربع في القاعدة، طول قطري القاعدة الأكبر 10 سم، بينما الأصغر 6 سم، وطول الحافة 4 سم، عليك إيجاد الارتفاع. أولا نجد ساق واحدة: أ = (10-6)/2 = 2 سم، والساق الواحدة تساوي 2 سم، والوتر 4 سم، ويتبين أن الرجل الثانية أو الارتفاع سيكون يساوي 16- 4 = 12، أي h = √12 = حوالي 3.5 سم.

عند حل المشكلة C2 باستخدام الطريقة الإحداثية، يواجه العديد من الطلاب نفس المشكلة. لا يمكنهم الحساب إحداثيات النقاطالمدرجة في صيغة المنتج العددية. تنشأ أكبر الصعوبات الأهرامات. وإذا كانت النقاط الأساسية تعتبر طبيعية إلى حد ما، فإن القمم هي جحيم حقيقي.

اليوم سنعمل على هرم رباعي الزوايا منتظم. ويوجد أيضًا هرم ثلاثي (ويعرف أيضًا باسم - رباعي الاسطح). هذا تصميم أكثر تعقيدًا، لذا سيتم تخصيص درس منفصل له.

أولا، دعونا نتذكر التعريف:

الهرم المنتظم هو الذي:

1. القاعدة عبارة عن مضلع منتظم: مثلث، مربع، وما إلى ذلك؛
2. الارتفاع المرسوم إلى القاعدة يمر عبر مركزها.

على وجه الخصوص، قاعدة الهرم الرباعي مربع. تماما مثل خوفو، فقط أصغر قليلا.

فيما يلي حسابات الهرم الذي تساوي جميع أحرفه 1. إذا لم يكن هذا هو الحال في مشكلتك، فلن تتغير الحسابات - فقط الأرقام ستكون مختلفة.

رؤوس الهرم الرباعي

لذا، لنفترض أن SABCD هرم رباعي الزوايا منتظم، حيث S هو الرأس والقاعدة ABCD هي مربع. جميع الحواف تساوي 1. تحتاج إلى إدخال نظام إحداثيات والعثور على إحداثيات جميع النقاط. لدينا:

نقدم نظام الإحداثيات مع الأصل عند النقطة A:

1. يتم توجيه محور OX بالتوازي مع الحافة AB؛
2. محور OY موازي لـ AD. بما أن ABCD مربع، AB ⊥ AD؛
3. وأخيرًا، نقوم بتوجيه محور OZ لأعلى، بشكل عمودي على المستوى ABCD.

الآن نحسب الإحداثيات. البناء الإضافي: SH - الارتفاع المرسوم على القاعدة. للراحة، سنضع قاعدة الهرم في رسم منفصل. بما أن النقاط A وB وC وD تقع في مستوى OXY، فإن إحداثياتها هي z = 0. لدينا:

1. أ = (0؛ 0؛ 0) - يتزامن مع الأصل؛
2. B = (1؛ 0؛ 0) - خطوة بخطوة 1 على طول محور OX من الأصل؛
3. C = (1؛ 1؛ 0) - خطوة بمقدار 1 على طول محور OX و1 على طول محور OY؛
4. D = (0; 1; 0) - خطوة فقط على طول محور OY.
5. H = (0.5; 0.5; 0) - مركز المربع، منتصف القطعة AC.

يبقى العثور على إحداثيات النقطة S. لاحظ أن إحداثيات x وy للنقطتين S وH متماثلتان، حيث أنهما تقعان على خط موازٍ لمحور OZ. يبقى العثور على الإحداثي z للنقطة S.

النظر في المثلثين ASH وABH:

1. AS = AB = 1 حسب الحالة؛
2. الزاوية AHS = AHB = 90°، بما أن SH هو الارتفاع وAH ⊥ HB هما قطرا المربع؛
3. الجانب AH شائع.

لذلك، المثلثان القائمان ASH و ABH متساويساق واحدة ووتر واحد لكل منهما. وهذا يعني SH = BH = 0.5 دينار بحريني. لكن BD هو قطر المربع الذي طول ضلعه 1. لذلك لدينا:

الإحداثيات الإجمالية للنقطة S:

في الختام، نكتب إحداثيات جميع رؤوس الهرم المستطيل المنتظم:

ماذا تفعل عندما تكون الأضلاع مختلفة

ماذا لو كانت الحواف الجانبية للهرم غير متساوية مع حواف القاعدة؟ في هذه الحالة، فكر في المثلث AHS:

مثلث AHS - مستطيلي، والوتر AS هو أيضًا حافة جانبية للهرم الأصلي SABCD. يتم حساب الساق AH بسهولة: AH = 0.5 AC. سوف نجد الساق المتبقية SH وفقا لنظرية فيثاغورس. سيكون هذا هو الإحداثي z للنقطة S.

مهمة. بالنظر إلى هرم رباعي الزوايا منتظم SABCD، يوجد في قاعدته مربع ذو ضلع 1. الحافة الجانبية BS = 3. أوجد إحداثيات النقطة S.

نحن نعرف بالفعل إحداثيات x وy لهذه النقطة: x = y = 0.5. ويأتي ذلك من حقيقتين:

1. إسقاط النقطة S على مستوى OXY هو النقطة H؛
2. وفي الوقت نفسه، النقطة H هي مركز المربع ABCD، الذي تساوي جميع أضلاعه 1.

يبقى العثور على إحداثيات النقطة S. النظر في المثلث AHS. وهو مستطيل، مع الوتر AS = BS = 3، والضلع AH هو نصف القطر. لمزيد من الحسابات نحتاج إلى طوله:

نظرية فيثاغورس للمثلث AHS: AH 2 + SH 2 = AS 2. لدينا:

إذن إحداثيات النقطة S: