Τριγωνικός τύπος πυραμίδας. Πυραμίδα. Πόροι του Διαδικτύου

Έννοια της πυραμίδας

Ορισμός 1

Ένα γεωμετρικό σχήμα που σχηματίζεται από ένα πολύγωνο και ένα σημείο που δεν βρίσκεται στο επίπεδο που περιέχει αυτό το πολύγωνο, συνδεδεμένο με όλες τις κορυφές του πολυγώνου, ονομάζεται πυραμίδα (Εικ. 1).

Το πολύγωνο από το οποίο αποτελείται η πυραμίδα ονομάζεται βάση της πυραμίδας· τα τρίγωνα που προκύπτουν, όταν συνδέονται με ένα σημείο, είναι οι πλευρικές όψεις της πυραμίδας, οι πλευρές των τριγώνων είναι οι πλευρές της πυραμίδας και το κοινό σημείο σε όλα τα τρίγωνα βρίσκεται η κορυφή της πυραμίδας.

Τύποι πυραμίδων

Ανάλογα με τον αριθμό των γωνιών στη βάση της πυραμίδας, μπορεί να ονομαστεί τριγωνική, τετραγωνική και ούτω καθεξής (Εικ. 2).

Σχήμα 2.

Ένας άλλος τύπος πυραμίδας είναι η κανονική πυραμίδα.

Ας εισαγάγουμε και ας αποδείξουμε την ιδιότητα μιας κανονικής πυραμίδας.

Θεώρημα 1

Όλες οι πλευρικές όψεις μιας κανονικής πυραμίδας είναι ισοσκελές τρίγωνα που είναι ίσα μεταξύ τους.

Απόδειξη.

Θεωρήστε μια κανονική $n-$gonal πυραμίδα με κορυφή $S$ ύψους $h=SO$. Ας σχεδιάσουμε έναν κύκλο γύρω από τη βάση (Εικ. 4).

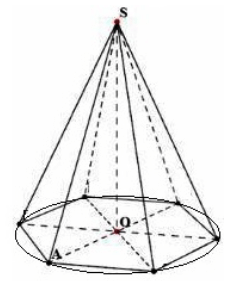
Εικόνα 4.

Θεωρήστε το τρίγωνο $SOA$. Σύμφωνα με το Πυθαγόρειο θεώρημα, παίρνουμε

Προφανώς, κάθε πλευρικό άκρο θα οριστεί με αυτόν τον τρόπο. Κατά συνέπεια, όλες οι πλευρικές ακμές είναι ίσες μεταξύ τους, δηλαδή όλες οι πλευρικές όψεις είναι ισοσκελές τρίγωνα. Ας αποδείξουμε ότι είναι ίσοι μεταξύ τους. Δεδομένου ότι η βάση είναι ένα κανονικό πολύγωνο, οι βάσεις όλων των πλευρικών όψεων είναι ίσες μεταξύ τους. Κατά συνέπεια, όλες οι πλευρικές όψεις είναι ίσες σύμφωνα με το III κριτήριο της ισότητας των τριγώνων.

Το θεώρημα έχει αποδειχθεί.

Ας εισαγάγουμε τώρα τον ακόλουθο ορισμό που σχετίζεται με την έννοια της κανονικής πυραμίδας.

Ορισμός 3

Το απόθεμα μιας κανονικής πυραμίδας είναι το ύψος της πλευρικής της όψης.

Προφανώς, από το Θεώρημα Πρώτο, όλα τα αποθέματα είναι ίσα μεταξύ τους.

Θεώρημα 2

Η πλευρική επιφάνεια μιας κανονικής πυραμίδας προσδιορίζεται ως το γινόμενο της ημιπεριμέτρου της βάσης και του αποθέματος.

Απόδειξη.

Ας υποδηλώσουμε την πλευρά της βάσης της $n-$gonal πυραμίδας με $a$ και το απόθεμα με $d$. Επομένως, η περιοχή της πλευρικής όψης είναι ίση με

Αφού, σύμφωνα με το Θεώρημα 1, όλες οι πλευρές είναι ίσες, τότε

Το θεώρημα έχει αποδειχθεί.

Ένας άλλος τύπος πυραμίδας είναι μια κολοβωμένη πυραμίδα.

Ορισμός 4

Εάν ένα επίπεδο παράλληλο προς τη βάση του τραβηχτεί μέσω μιας συνηθισμένης πυραμίδας, τότε το σχήμα που σχηματίζεται μεταξύ αυτού του επιπέδου και του επιπέδου της βάσης ονομάζεται κολοβωμένη πυραμίδα (Εικ. 5).

Εικόνα 5. Κόλουρη πυραμίδα

Οι πλευρικές όψεις της κολοβωμένης πυραμίδας είναι τραπεζοειδείς.

Θεώρημα 3

Το εμβαδόν της πλευρικής επιφάνειας μιας κανονικής κολοβωμένης πυραμίδας προσδιορίζεται ως το γινόμενο του αθροίσματος των ημιπεριμέτρων των βάσεων και του αποθέματος.

Απόδειξη.

Ας υποδηλώσουμε τις πλευρές των βάσεων της πυραμίδας $n-$gonal με $a\ και\ b$, αντίστοιχα, και το απόθεμα με $d$. Επομένως, η περιοχή της πλευρικής όψης είναι ίση με

Αφού όλες οι πλευρές είναι ίσες, λοιπόν

Το θεώρημα έχει αποδειχθεί.

Δείγμα εργασίας

Παράδειγμα 1

Βρείτε το εμβαδόν της πλευρικής επιφάνειας μιας κόλουρης τριγωνικής πυραμίδας εάν λαμβάνεται από μια κανονική πυραμίδα με πλευρά βάσης 4 και απόθεμα 5 κόβοντας ένα επίπεδο που διέρχεται από τη μέση γραμμή των πλευρικών όψεων.

Λύση.

Χρησιμοποιώντας το θεώρημα της μέσης γραμμής, βρίσκουμε ότι η άνω βάση της κολοβωμένης πυραμίδας είναι ίση με $4\cdot \frac(1)(2)=2$ και το απόθεμα είναι ίσο με $5\cdot \frac(1)(2) =2,5$.

Στη συνέχεια, με το Θεώρημα 3, παίρνουμε

Ορισμός

Πυραμίδαείναι ένα πολύεδρο που αποτελείται από ένα πολύγωνο \(A_1A_2...A_n\) και \(n\) τρίγωνα με κοινή κορυφή \(P\) (δεν βρίσκεται στο επίπεδο του πολυγώνου) και πλευρές απέναντι από αυτό, που συμπίπτουν με την πλευρές του πολυγώνου.
Ονομασία: \(PA_1A_2...A_n\) .
Παράδειγμα: πενταγωνική πυραμίδα \(PA_1A_2A_3A_4A_5\) .

Τρίγωνα \(PA_1A_2, \PA_2A_3\), κ.λπ. λέγονται πλαϊνά πρόσωπαπυραμίδες, τμήματα \(PA_1, PA_2\) κ.λπ. – πλευρικές νευρώσεις, πολύγωνο \(A_1A_2A_3A_4A_5\) – βάση, σημείο \(P\) – μπλουζα.

ΥψοςΟι πυραμίδες είναι μια κάθετη που κατεβαίνει από την κορυφή της πυραμίδας στο επίπεδο της βάσης.

Μια πυραμίδα με ένα τρίγωνο στη βάση της ονομάζεται τετράεδρο.

Η πυραμίδα ονομάζεται σωστός, εάν η βάση του είναι κανονικό πολύγωνο και πληρούται μία από τις ακόλουθες προϋποθέσεις:

\((α)\) οι πλευρικές άκρες της πυραμίδας είναι ίσες.

\((β)\) το ύψος της πυραμίδας διέρχεται από το κέντρο του κύκλου που περιβάλλεται κοντά στη βάση.

\((γ)\) οι πλευρικές νευρώσεις έχουν κλίση προς το επίπεδο της βάσης στην ίδια γωνία.

\((δ)\) οι πλευρικές όψεις είναι κεκλιμένες προς το επίπεδο της βάσης στην ίδια γωνία.

Κανονικό τετράεδροείναι μια τριγωνική πυραμίδα, της οποίας όλες οι όψεις είναι ίσα ισόπλευρα τρίγωνα.

Θεώρημα

Οι συνθήκες \((α), (β), (γ), (δ)\) είναι ισοδύναμες.

Απόδειξη

Ας βρούμε το ύψος της πυραμίδας \(PH\) . Έστω \(\άλφα\) το επίπεδο της βάσης της πυραμίδας.

1) Ας αποδείξουμε ότι από το \((a)\) προκύπτει \((b)\) . Έστω \(PA_1=PA_2=PA_3=...=PA_n\) .

Επειδή \(PH\perp \alpha\), τότε το \(PH\) είναι κάθετο σε οποιαδήποτε ευθεία βρίσκεται σε αυτό το επίπεδο, πράγμα που σημαίνει ότι τα τρίγωνα είναι ορθογώνια. Αυτό σημαίνει ότι αυτά τα τρίγωνα είναι ίσα στο κοινό σκέλος \(PH\) και στην υποτείνουσα \(PA_1=PA_2=PA_3=...=PA_n\) . Αυτό σημαίνει \(A_1H=A_2H=...=A_nH\) . Αυτό σημαίνει ότι τα σημεία \(A_1, A_2, ..., A_n\) βρίσκονται στην ίδια απόσταση από το σημείο \(H\), επομένως, βρίσκονται στον ίδιο κύκλο με την ακτίνα \(A_1H\) . Αυτός ο κύκλος, εξ ορισμού, περικλείεται στο πολύγωνο \(A_1A_2...A_n\) .

2) Ας αποδείξουμε ότι το \((b)\) υποδηλώνει \((c)\) .

\(PA_1H, PA_2H, PA_3H,..., PA_nH\)ορθογώνιο και ίσο σε δύο πόδια. Αυτό σημαίνει ότι οι γωνίες τους είναι επίσης ίσες, επομένως, \(\γωνία PA_1H=\γωνία PA_2H=...=\γωνία PA_nH\).

3) Ας αποδείξουμε ότι το \((c)\) υποδηλώνει \((a)\) .

Παρόμοια με το πρώτο σημείο, τρίγωνα \(PA_1H, PA_2H, PA_3H,..., PA_nH\)ορθογώνια τόσο κατά μήκος του ποδιού όσο και οξεία γωνία. Αυτό σημαίνει ότι και οι υποτείνυσές τους είναι ίσες, δηλαδή \(PA_1=PA_2=PA_3=...=PA_n\) .

4) Ας αποδείξουμε ότι το \((b)\) υποδηλώνει \((d)\) .

Επειδή Σε ένα κανονικό πολύγωνο τα κέντρα των περιγεγραμμένων και εγγεγραμμένων κύκλων συμπίπτουν (γενικά μιλώντας, αυτό το σημείο ονομάζεται κέντρο ενός κανονικού πολυγώνου), τότε το \(H\) είναι το κέντρο του εγγεγραμμένου κύκλου. Ας σχεδιάσουμε κάθετες από το σημείο \(H\) στις πλευρές της βάσης: \(HK_1, HK_2\), κ.λπ. Αυτές είναι οι ακτίνες του εγγεγραμμένου κύκλου (εξ ορισμού). Στη συνέχεια, σύμφωνα με το TTP (το \(PH\) είναι κάθετο στο επίπεδο, \(HK_1, HK_2\), κ.λπ. είναι προεξοχές κάθετες στις πλευρές) με κλίση \(PK_1, PK_2\), κ.λπ. κάθετες στις πλευρές \(A_1A_2, A_2A_3\), κ.λπ. αντίστοιχα. Έτσι, εξ ορισμού \(\γωνία PK_1H, \γωνία PK_2H\)ίσες με τις γωνίες μεταξύ των πλευρικών όψεων και της βάσης. Επειδή τα τρίγωνα \(PK_1H, PK_2H, ...\) είναι ίσα (ως ορθογώνια σε δύο πλευρές), τότε οι γωνίες \(\γωνία PK_1H, \γωνία PK_2H, ...\)είναι ίσα.

5) Ας αποδείξουμε ότι το \((d)\) υποδηλώνει \((b)\) .

Παρόμοια με το τέταρτο σημείο, τα τρίγωνα \(PK_1H, PK_2H, ...\) είναι ίσα (ως ορθογώνια κατά μήκος του σκέλους και οξεία γωνία), που σημαίνει ότι τα τμήματα \(HK_1=HK_2=...=HK_n\) είναι ίσος. Αυτό σημαίνει, εξ ορισμού, το \(H\) είναι το κέντρο ενός κύκλου που είναι εγγεγραμμένο στη βάση. Αλλά επειδή Για κανονικά πολύγωνα, τα κέντρα των εγγεγραμμένων και περιγεγραμμένων κύκλων συμπίπτουν, τότε το \(H\) είναι το κέντρο του περιγεγραμμένου κύκλου. Chtd.

Συνέπεια

Οι πλευρικές όψεις μιας κανονικής πυραμίδας είναι ίσα ισοσκελές τρίγωνα.

Ορισμός

Το ύψος της πλευρικής όψης μιας κανονικής πυραμίδας που αντλείται από την κορυφή της ονομάζεται αποθεμα.
Τα αποθέματα όλων των πλευρικών όψεων μιας κανονικής πυραμίδας είναι ίσα μεταξύ τους και είναι επίσης διάμεσοι και διχοτόμοι.

Σημαντικές σημειώσεις

1. Το ύψος μιας κανονικής τριγωνικής πυραμίδας πέφτει στο σημείο τομής των υψών (ή διχοτόμων, ή διαμέσου) της βάσης (η βάση είναι κανονικό τρίγωνο).

2. Το ύψος μιας κανονικής τετραγωνικής πυραμίδας πέφτει στο σημείο τομής των διαγωνίων της βάσης (η βάση είναι τετράγωνο).

3. Το ύψος μιας κανονικής εξαγωνικής πυραμίδας πέφτει στο σημείο τομής των διαγωνίων της βάσης (η βάση είναι κανονικό εξάγωνο).

4. Το ύψος της πυραμίδας είναι κάθετο σε κάθε ευθεία που βρίσκεται στη βάση.

Ορισμός

Η πυραμίδα ονομάζεται ορθογώνιος, αν ένα από τα πλευρικά άκρα του είναι κάθετο στο επίπεδο της βάσης.

Σημαντικές σημειώσεις

1. Σε μια ορθογώνια πυραμίδα, η άκρη κάθετη στη βάση είναι το ύψος της πυραμίδας. Δηλαδή, \(SR\) είναι το ύψος.

2. Επειδή Το \(SR\) είναι κάθετο σε οποιαδήποτε γραμμή από τη βάση, λοιπόν \(\triangle SRM, \triangle SRP\)– ορθογώνια τρίγωνα.

3. Τρίγωνα \(\τρίγωνο SRN, \τρίγωνο SRK\)- επίσης ορθογώνιο.
Δηλαδή, κάθε τρίγωνο που σχηματίζεται από αυτή την άκρη και η διαγώνιος που αναδύεται από την κορυφή αυτής της ακμής που βρίσκεται στη βάση θα είναι ορθογώνιο.

\[(\Large(\text(Όγκος και επιφάνεια της πυραμίδας)))\]

Θεώρημα

Ο όγκος της πυραμίδας είναι ίσος με το ένα τρίτο του γινομένου του εμβαδού της βάσης και του ύψους της πυραμίδας: \

Συνέπειες

Έστω \(a\) η πλευρά της βάσης, \(h\) το ύψος της πυραμίδας.

1. Ο όγκος μιας κανονικής τριγωνικής πυραμίδας είναι \(V_(\text(δεξιό τρίγωνο.pir.))=\dfrac(\sqrt3)(12)a^2h\),

2. Ο όγκος μιας κανονικής τετραγωνικής πυραμίδας είναι \(V_(\text(right.four.pir.))=\dfrac13a^2h\).

3. Ο όγκος μιας κανονικής εξαγωνικής πυραμίδας είναι \(V_(\text(right.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).

4. Ο όγκος ενός κανονικού τετραέδρου είναι \(V_(\text(δεξιά tetr.))=\dfrac(\sqrt3)(12)a^3\).

Θεώρημα

Το εμβαδόν της πλευρικής επιφάνειας μιας κανονικής πυραμίδας είναι ίσο με το μισό γινόμενο της περιμέτρου της βάσης και του αποθέματος.

\[(\Large(\text(Frustum)))\]

Ορισμός

Σκεφτείτε μια αυθαίρετη πυραμίδα \(PA_1A_2A_3...A_n\) . Ας σχεδιάσουμε ένα επίπεδο παράλληλο στη βάση της πυραμίδας μέσα από ένα συγκεκριμένο σημείο που βρίσκεται στο πλευρικό άκρο της πυραμίδας. Αυτό το επίπεδο θα χωρίσει την πυραμίδα σε δύο πολύεδρα, το ένα από τα οποία είναι πυραμίδα (\(PB_1B_2...B_n\)) και το άλλο ονομάζεται κολοβωμένη πυραμίδα(\(A_1A_2...A_nB_1B_2...B_n\) ).

Η κολοβωμένη πυραμίδα έχει δύο βάσεις - πολύγωνα \(A_1A_2...A_n\) και \(B_1B_2...B_n\) που είναι παρόμοια μεταξύ τους.

Το ύψος μιας κόλουρης πυραμίδας είναι μια κάθετη που τραβιέται από κάποιο σημείο της άνω βάσης στο επίπεδο της κάτω βάσης.

Σημαντικές σημειώσεις

1. Όλες οι πλευρικές όψεις μιας κολοβωμένης πυραμίδας είναι τραπεζοειδή.

2. Το τμήμα που συνδέει τα κέντρα των βάσεων μιας κανονικής κόλουρης πυραμίδας (δηλαδή μιας πυραμίδας που προκύπτει από διατομή μιας κανονικής πυραμίδας) είναι το ύψος.

Όταν ένα άτομο ακούει τη λέξη «πυραμίδα», θυμάται αμέσως τις μεγαλοπρεπείς αιγυπτιακές κατασκευές. Ωστόσο, οι αρχαίοι πέτρινοι γίγαντες είναι μόνο ένας από τους εκπροσώπους της τάξης των πυραμίδων. Σε αυτό το άρθρο θα εξετάσουμε από γεωμετρική άποψη τις ιδιότητες μιας κανονικής τετραγωνικής πυραμίδας.

Τι είναι μια πυραμίδα γενικά;

Στη γεωμετρία, νοείται ως ένα τρισδιάστατο σχήμα, το οποίο μπορεί να ληφθεί συνδέοντας όλες τις κορυφές ενός επίπεδου πολυγώνου με ένα μόνο σημείο που βρίσκεται σε διαφορετικό επίπεδο από αυτό το πολύγωνο. Το παρακάτω σχήμα δείχνει 4 σχήματα που πληρούν αυτόν τον ορισμό.

Βλέπουμε ότι το πρώτο σχήμα έχει τριγωνική βάση, το δεύτερο έχει τετράγωνη βάση. Τα δύο τελευταία αντιπροσωπεύονται από πενταγωνική και εξαγωνική βάση. Ωστόσο, η πλευρική επιφάνεια όλων των πυραμίδων σχηματίζεται από τρίγωνα. Ο αριθμός τους είναι ακριβώς ίσος με τον αριθμό των πλευρών ή των κορυφών του πολυγώνου στη βάση.

Ένας ειδικός τύπος πυραμίδας, που διαφέρει από τους άλλους εκπροσώπους της τάξης στην ιδανική συμμετρία της, είναι η κανονική πυραμίδα. Για να είναι σωστό το σχήμα, πρέπει να πληρούνται οι ακόλουθες δύο προϋποθέσεις:

• η βάση πρέπει να έχει κανονικό πολύγωνο.
• η πλευρική επιφάνεια του σχήματος πρέπει να αποτελείται από ίσα ισοσκελή τρίγωνα.

Σημειώστε ότι η δεύτερη υποχρεωτική συνθήκη μπορεί να αντικατασταθεί από μια άλλη: μια κάθετη που τραβιέται στη βάση από την κορυφή της πυραμίδας (το σημείο τομής των πλευρικών τριγώνων) πρέπει να τέμνει αυτή τη βάση στο γεωμετρικό της κέντρο.

Τώρα ας προχωρήσουμε στο θέμα του άρθρου και ας εξετάσουμε ποιες ιδιότητες μιας κανονικής τετραγωνικής πυραμίδας τη χαρακτηρίζουν. Αρχικά, ας δείξουμε στο σχήμα πώς μοιάζει αυτό το σχήμα.

Η βάση του είναι τετράγωνο. Οι πλευρές αντιπροσωπεύουν 4 όμοια ισοσκελή τρίγωνα (μπορούν επίσης να είναι ισόπλευρα σε ορισμένο λόγο του μήκους της πλευράς του τετραγώνου και του ύψους του σχήματος). Το ύψος που θα χαμηλώσει από την κορυφή της πυραμίδας θα τέμνει το τετράγωνο στο κέντρο της (το σημείο τομής των διαγωνίων).

Αυτή η πυραμίδα έχει 5 όψεις (ένα τετράγωνο και τέσσερα τρίγωνα), 5 κορυφές (τέσσερις από αυτές ανήκουν στη βάση) και 8 άκρες. τέταρτη τάξη, περνώντας από το ύψος της πυραμίδας, τη μεταμορφώνει στον εαυτό της περιστρέφοντας 90 ο.

Οι αιγυπτιακές πυραμίδες στη Γκίζα είναι κανονικές τετράγωνες.

Τέσσερις Βασικές Γραμμικές Παράμετροι

Ας ξεκινήσουμε την εξέταση των μαθηματικών ιδιοτήτων μιας κανονικής τετραγωνικής πυραμίδας με τους τύπους για το ύψος, το μήκος πλευράς της βάσης, το πλευρικό άκρο και το απόθεμα. Ας πούμε αμέσως ότι όλες αυτές οι ποσότητες σχετίζονται μεταξύ τους, οπότε αρκεί να γνωρίζουμε μόνο δύο από αυτές για να υπολογίσουμε με σαφήνεια τις υπόλοιπες δύο.

Ας υποθέσουμε ότι το ύψος h της πυραμίδας και το μήκος a της πλευράς της τετραγωνικής βάσης είναι γνωστά, τότε η πλευρική ακμή b θα είναι ίση με:

b = √(a 2 / 2 + h 2)

Τώρα δίνουμε τον τύπο για το μήκος a b του αποθέματος (το ύψος του τριγώνου που έχει χαμηλώσει στην πλευρά της βάσης):

a b = √(a 2 / 4 + h 2)

Προφανώς, η πλευρική ακμή b είναι πάντα μεγαλύτερη από το απόθεμα a b .

Και οι δύο εκφράσεις μπορούν να χρησιμοποιηθούν για τον προσδιορισμό και των τεσσάρων γραμμικών χαρακτηριστικών εάν οι άλλες δύο παράμετροι είναι γνωστές, για παράδειγμα a b και h.

Εμβαδόν και όγκος σχήματος

Αυτές είναι δύο ακόμη σημαντικές ιδιότητες μιας κανονικής τετραγωνικής πυραμίδας. Η βάση του σχήματος έχει την εξής περιοχή:

Κάθε μαθητής γνωρίζει αυτή τη φόρμουλα. Το εμβαδόν της πλευρικής επιφάνειας, που σχηματίζεται από τέσσερα ίδια τρίγωνα, μπορεί να προσδιοριστεί μέσω του αποθέματος a b της πυραμίδας ως εξής:

Εάν το a b είναι άγνωστο, τότε μπορεί να προσδιοριστεί χρησιμοποιώντας τους τύπους της προηγούμενης παραγράφου μέχρι το ύψος h ή την ακμή b.

Η συνολική επιφάνεια του σχήματος που εξετάζουμε είναι το άθροισμα των περιοχών S o και S b:

S = S o + S b = a 2 + 2 × a × a b = a (a + 2 × a b)

Η υπολογισμένη περιοχή όλων των όψεων της πυραμίδας φαίνεται στο παρακάτω σχήμα με τη μορφή της ανάπτυξής της.

Μια περιγραφή των ιδιοτήτων μιας κανονικής τετραγωνικής πυραμίδας δεν θα είναι πλήρης χωρίς να ληφθεί υπόψη ο τύπος για τον προσδιορισμό του όγκου της. Αυτή η τιμή για την εν λόγω πυραμίδα υπολογίζεται ως εξής:

Δηλαδή, το V είναι ίσο με το τρίτο μέρος του γινομένου του ύψους του σχήματος και του εμβαδού της βάσης του.

Ιδιότητες κανονικής κόλουρης τετραγωνικής πυραμίδας

Μπορείτε να πάρετε αυτό το σχήμα από την αρχική πυραμίδα. Για να το κάνετε αυτό, πρέπει να κόψετε την κορυφή της πυραμίδας με ένα αεροπλάνο. Η φιγούρα που παραμένει κάτω από το κομμένο επίπεδο θα ονομάζεται κολοβωμένη πυραμίδα.

Είναι πιο βολικό να μελετήσουμε τα χαρακτηριστικά μιας κολοβωμένης πυραμίδας εάν οι βάσεις της είναι παράλληλες μεταξύ τους. Σε αυτήν την περίπτωση, η κάτω και η πάνω βάση θα είναι παρόμοια πολύγωνα. Δεδομένου ότι σε μια τετραγωνική κανονική πυραμίδα η βάση είναι ένα τετράγωνο, το τμήμα που σχηματίζεται κατά την κοπή θα αντιπροσωπεύει επίσης ένα τετράγωνο, αλλά μικρότερου μεγέθους.

Η πλευρική επιφάνεια του κόλουρου σχήματος σχηματίζεται όχι από τρίγωνα, αλλά από ισοσκελή τραπεζοειδή.

Μία από τις σημαντικές ιδιότητες αυτής της πυραμίδας είναι ο όγκος της, ο οποίος υπολογίζεται από τον τύπο:

V = 1/3 × h × (S o1 + S o2 + √(S o1 × S o2))

Εδώ h είναι η απόσταση μεταξύ των βάσεων του σχήματος, S o1, S o2 είναι οι περιοχές της κάτω και της άνω βάσης.

Μια πυραμίδα είναι ένα πολύεδρο με ένα πολύγωνο στη βάση του. Όλες οι όψεις, με τη σειρά τους, σχηματίζουν τρίγωνα που συγκλίνουν σε μία κορυφή. Οι πυραμίδες είναι τριγωνικές, τετράγωνες και ούτω καθεξής. Για να προσδιορίσετε ποια πυραμίδα βρίσκεται μπροστά σας, αρκεί να μετρήσετε τον αριθμό των γωνιών στη βάση της. Ο ορισμός του «ύψους πυραμίδας» βρίσκεται πολύ συχνά σε προβλήματα γεωμετρίας στο σχολικό πρόγραμμα σπουδών. Σε αυτό το άρθρο θα προσπαθήσουμε να δούμε διαφορετικούς τρόπους για να το βρούμε.

Τμήματα της πυραμίδας

Κάθε πυραμίδα αποτελείται από τα ακόλουθα στοιχεία:

• πλευρικές όψεις, που έχουν τρεις γωνίες και συγκλίνουν στην κορυφή.
• το απόθεμα αντιπροσωπεύει το ύψος που κατεβαίνει από την κορυφή του.
• η κορυφή της πυραμίδας είναι ένα σημείο που συνδέει τις πλευρικές νευρώσεις, αλλά δεν βρίσκεται στο επίπεδο της βάσης.
• η βάση είναι ένα πολύγωνο στο οποίο δεν βρίσκεται η κορυφή.
• το ύψος μιας πυραμίδας είναι ένα τμήμα που τέμνει την κορυφή της πυραμίδας και σχηματίζει ορθή γωνία με τη βάση της.

Πώς να βρείτε το ύψος μιας πυραμίδας αν είναι γνωστός ο όγκος της

Μέσω του τύπου V = (S*h)/3 (στον τύπο V είναι ο όγκος, S είναι το εμβαδόν της βάσης, h είναι το ύψος της πυραμίδας) βρίσκουμε ότι h = (3*V)/ ΜΙΚΡΟ. Για να εμπεδώσουμε το υλικό, ας λύσουμε αμέσως το πρόβλημα. Η τριγωνική βάση είναι 50 cm 2 , ενώ ο όγκος της είναι 125 cm 3 . Το ύψος της τριγωνικής πυραμίδας είναι άγνωστο, αυτό που πρέπει να βρούμε. Όλα είναι απλά εδώ: εισάγουμε τα δεδομένα στον τύπο μας. Παίρνουμε h = (3*125)/50 = 7,5 cm.

Πώς να βρείτε το ύψος μιας πυραμίδας εάν είναι γνωστό το μήκος της διαγωνίου και τα άκρα της

Όπως θυμόμαστε, το ύψος της πυραμίδας σχηματίζει ορθή γωνία με τη βάση της. Αυτό σημαίνει ότι το ύψος, η άκρη και το μισό της διαγωνίου μαζί σχηματίζουν Πολλοί, φυσικά, θυμούνται το Πυθαγόρειο θεώρημα. Γνωρίζοντας δύο διαστάσεις, δεν θα είναι δύσκολο να βρείτε την τρίτη ποσότητα. Ας θυμηθούμε το γνωστό θεώρημα a² = b² + c², όπου a είναι η υποτείνουσα και στην περίπτωσή μας η άκρη της πυραμίδας. β - το πρώτο σκέλος ή το μισό της διαγωνίου και c - αντίστοιχα, το δεύτερο σκέλος ή το ύψος της πυραμίδας. Από αυτόν τον τύπο c² = a² - b².

Τώρα το πρόβλημα: σε μια κανονική πυραμίδα η διαγώνιος είναι 20 εκ., όταν το μήκος της άκρης είναι 30 εκ. Πρέπει να βρείτε το ύψος. Λύνουμε: c² = 30² - 20² = 900-400 = 500. Επομένως c = √ 500 = περίπου 22,4.

Πώς να βρείτε το ύψος μιας κολοβωμένης πυραμίδας

Είναι ένα πολύγωνο με διατομή παράλληλη στη βάση του. Το ύψος μιας κολοβωμένης πυραμίδας είναι το τμήμα που συνδέει τις δύο βάσεις της. Το ύψος μπορεί να βρεθεί για μια κανονική πυραμίδα εάν είναι γνωστά τα μήκη των διαγωνίων και των δύο βάσεων, καθώς και η άκρη της πυραμίδας. Έστω η διαγώνιος της μεγαλύτερης βάσης d1, ενώ η διαγώνιος της μικρότερης βάσης είναι d2, και η άκρη έχει μήκος l. Για να βρείτε το ύψος, μπορείτε να χαμηλώσετε τα ύψη από τα δύο επάνω απέναντι σημεία του διαγράμματος στη βάση του. Βλέπουμε ότι έχουμε δύο ορθογώνια τρίγωνα, το μόνο που μένει είναι να βρούμε τα μήκη των ποδιών τους. Για να το κάνετε αυτό, αφαιρέστε τη μικρότερη από τη μεγαλύτερη διαγώνιο και διαιρέστε με το 2. Έτσι θα βρούμε ένα σκέλος: a = (d1-d2)/2. Μετά από αυτό, σύμφωνα με το Πυθαγόρειο θεώρημα, το μόνο που έχουμε να κάνουμε είναι να βρούμε το δεύτερο σκέλος, που είναι το ύψος της πυραμίδας.

Τώρα ας το δούμε όλο αυτό στην πράξη. Έχουμε ένα έργο μπροστά μας. Μια κολοβωμένη πυραμίδα έχει ένα τετράγωνο στη βάση, το διαγώνιο μήκος της μεγαλύτερης βάσης είναι 10 εκ., ενώ της μικρότερης είναι 6 εκ. και η άκρη είναι 4 εκ. Πρέπει να βρείτε το ύψος. Πρώτον, βρίσκουμε ένα πόδι: a = (10-6)/2 = 2 εκ. Το ένα πόδι είναι ίσο με 2 εκ. και η υποτείνουσα είναι 4 εκ. Αποδεικνύεται ότι το δεύτερο πόδι ή το ύψος θα είναι ίσο με 16- 4 = 12, δηλαδή h = √12 = περίπου 3,5 cm.

Κατά την επίλυση του Προβλήματος Γ2 χρησιμοποιώντας τη μέθοδο συντεταγμένων, πολλοί μαθητές αντιμετωπίζουν το ίδιο πρόβλημα. Δεν μπορούν να υπολογίσουν συντεταγμένες σημείωνπεριλαμβάνονται στη φόρμουλα βαθμωτών προϊόντων. Προκύπτουν οι μεγαλύτερες δυσκολίες πυραμίδες. Και αν τα σημεία βάσης θεωρούνται λίγο πολύ φυσιολογικά, τότε οι κορυφές είναι μια πραγματική κόλαση.

Σήμερα θα δουλέψουμε σε μια κανονική τετραγωνική πυραμίδα. Υπάρχει επίσης μια τριγωνική πυραμίδα (γνωστός και ως - τετράεδρο). Αυτός είναι ένας πιο περίπλοκος σχεδιασμός, επομένως θα αφιερωθεί ένα ξεχωριστό μάθημα σε αυτό.

Αρχικά, ας θυμηθούμε τον ορισμό:

Μια κανονική πυραμίδα είναι αυτή που:

1. Η βάση είναι ένα κανονικό πολύγωνο: τρίγωνο, τετράγωνο κ.λπ.
2. Ένα υψόμετρο που τραβιέται προς τη βάση διέρχεται από το κέντρο της.

Συγκεκριμένα, η βάση μιας τετράπλευρης πυραμίδας είναι τετράγωνο. Ακριβώς όπως ο Χέοπας, μόνο λίγο μικρότερος.

Παρακάτω είναι οι υπολογισμοί για μια πυραμίδα στην οποία όλες οι ακμές είναι ίσες με 1. Εάν δεν συμβαίνει αυτό στο πρόβλημά σας, οι υπολογισμοί δεν αλλάζουν - απλώς οι αριθμοί θα είναι διαφορετικοί.

Κορυφές τετράπλευρης πυραμίδας

Ας δοθεί λοιπόν μια κανονική τετραγωνική πυραμίδα SABCD, όπου S είναι η κορυφή και η βάση ABCD είναι τετράγωνο. Όλες οι ακμές είναι ίσες με 1. Πρέπει να εισαγάγετε ένα σύστημα συντεταγμένων και να βρείτε τις συντεταγμένες όλων των σημείων. Εχουμε:

Εισάγουμε ένα σύστημα συντεταγμένων με προέλευση στο σημείο Α:

1. Ο άξονας OX κατευθύνεται παράλληλα προς το άκρο ΑΒ.
2. Ο άξονας OY είναι παράλληλος με το AD. Εφόσον το ABCD είναι τετράγωνο, το AB ⊥ AD;
3. Τέλος, κατευθύνουμε τον άξονα OZ προς τα πάνω, κάθετα στο επίπεδο ABCD.

Τώρα υπολογίζουμε τις συντεταγμένες. Πρόσθετη κατασκευή: SH - ύψος τραβηγμένο στη βάση. Για ευκολία, θα τοποθετήσουμε τη βάση της πυραμίδας σε ξεχωριστό σχέδιο. Εφόσον τα σημεία A, B, C και D βρίσκονται στο επίπεδο OXY, η συντεταγμένη τους είναι z = 0. Έχουμε:

1. A = (0; 0; 0) - συμπίπτει με την προέλευση.
2. B = (1; 0; 0) - βήμα προς 1 κατά μήκος του άξονα OX από την αρχή.
3. C = (1; 1; 0) - βήμα προς 1 κατά μήκος του άξονα OX και κατά 1 κατά μήκος του άξονα OY.
4. D = (0; 1; 0) - βήμα μόνο κατά μήκος του άξονα OY.
5. H = (0,5; 0,5; 0) - το κέντρο του τετραγώνου, το μέσο του τμήματος AC.

Μένει να βρούμε τις συντεταγμένες του σημείου S. Σημειώστε ότι οι συντεταγμένες x και y των σημείων S και H είναι ίδιες, αφού βρίσκονται σε μια ευθεία παράλληλη προς τον άξονα OZ. Απομένει να βρεθεί η συντεταγμένη z για το σημείο S.

Εξετάστε τα τρίγωνα ASH και ABH:

1. AS = AB = 1 κατά συνθήκη.
2. Γωνία AHS = AHB = 90°, αφού SH είναι το ύψος και AH ⊥ HB ως οι διαγώνιοι του τετραγώνου.
3. Η πλευρά AH είναι κοινή.

Επομένως, ορθογώνια τρίγωνα ASH και ABH ίσοςένα πόδι και μια υποτείνουσα το καθένα. Αυτό σημαίνει SH = BH = 0,5 BD. Αλλά το BD είναι η διαγώνιος ενός τετραγώνου με πλευρά 1. Επομένως έχουμε:

Συνολικές συντεταγμένες του σημείου S:

Συμπερασματικά, γράφουμε τις συντεταγμένες όλων των κορυφών μιας κανονικής ορθογώνιας πυραμίδας:

Τι να κάνετε όταν τα πλευρά είναι διαφορετικά

Τι γίνεται αν οι πλευρικές ακμές της πυραμίδας δεν είναι ίσες με τις άκρες της βάσης; Σε αυτήν την περίπτωση, θεωρήστε το τρίγωνο AHS:

Τρίγωνο AHS - ορθογώνιος, και η υποτείνουσα AS είναι επίσης ένα πλευρικό άκρο της αρχικής πυραμίδας SABCD. Το πόδι AH υπολογίζεται εύκολα: AH = 0,5 AC. Θα βρούμε το υπόλοιπο πόδι SH σύμφωνα με το Πυθαγόρειο θεώρημα. Αυτή θα είναι η συντεταγμένη z για το σημείο S.

Εργο. Δίνεται μια κανονική τετραγωνική πυραμίδα SABCD, στη βάση της οποίας βρίσκεται ένα τετράγωνο με πλευρά 1. Πλαϊνή ακμή BS = 3. Βρείτε τις συντεταγμένες του σημείου S.

Γνωρίζουμε ήδη τις συντεταγμένες x και y αυτού του σημείου: x = y = 0,5. Αυτό προκύπτει από δύο γεγονότα:

1. Η προβολή του σημείου S στο επίπεδο OXY είναι το σημείο H.
2. Ταυτόχρονα, το σημείο Η είναι το κέντρο ενός τετραγώνου ABCD, του οποίου όλες οι πλευρές είναι ίσες με 1.

Απομένει να βρεθεί η συντεταγμένη του σημείου S. Εξετάστε το τρίγωνο AHS. Είναι ορθογώνιο, με την υποτείνουσα AS = BS = 3, το πόδι AH να είναι το μισό της διαγώνιου. Για περαιτέρω υπολογισμούς χρειαζόμαστε το μήκος του:

Πυθαγόρειο θεώρημα για το τρίγωνο AHS: AH 2 + SH 2 = AS 2. Εχουμε:

Άρα, οι συντεταγμένες του σημείου S: