Formula e piramidës trekëndore. Piramida. Burimet e internetit

Koncepti i piramidës

Përkufizimi 1

Një figurë gjeometrike e formuar nga një shumëkëndësh dhe një pikë që nuk shtrihet në rrafshin që përmban këtë shumëkëndësh, e lidhur me të gjitha kulmet e shumëkëndëshit, quhet piramidë (Fig. 1).

Shumëkëndëshi nga i cili është bërë piramida quhet baza e piramidës; trekëndëshat që rezultojnë, kur lidhen me një pikë, janë faqet anësore të piramidës, anët e trekëndëshave janë anët e piramidës dhe pika e përbashkët për të gjithë trekëndëshat është maja e piramidës.

Llojet e piramidave

Në varësi të numrit të këndeve në bazën e piramidës, ajo mund të quhet trekëndore, katërkëndore, e kështu me radhë (Fig. 2).

Figura 2.

Një tjetër lloj piramide është piramida e rregullt.

Le të prezantojmë dhe provojmë vetinë e një piramide të rregullt.

Teorema 1

Të gjitha faqet anësore të një piramide të rregullt janë trekëndësha izoscelorë që janë të barabartë me njëri-tjetrin.

Dëshmi.

Konsideroni një piramidë të rregullt $n-$gonale me kulm $S$ të lartësisë $h=SO$. Le të vizatojmë një rreth rreth bazës (Fig. 4).

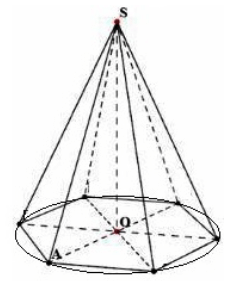
Figura 4.

Konsideroni trekëndëshin $SOA$. Sipas teoremës së Pitagorës, marrim

Natyrisht, çdo skaj anësor do të përcaktohet në këtë mënyrë. Rrjedhimisht, të gjitha skajet anësore janë të barabarta me njëra-tjetrën, domethënë, të gjitha faqet anësore janë trekëndësha dykëndësh. Le të vërtetojmë se janë të barabartë me njëri-tjetrin. Meqenëse baza është një shumëkëndësh i rregullt, bazat e të gjitha faqeve anësore janë të barabarta me njëra-tjetrën. Rrjedhimisht, të gjitha faqet anësore janë të barabarta sipas kriterit III të barazisë së trekëndëshave.

Teorema është vërtetuar.

Le të prezantojmë tani përkufizimin e mëposhtëm në lidhje me konceptin e një piramide të rregullt.

Përkufizimi 3

Apotema e një piramide të rregullt është lartësia e faqes anësore të saj.

Natyrisht, nga Teorema Një, të gjitha apotemat janë të barabarta me njëra-tjetrën.

Teorema 2

Sipërfaqja anësore e një piramide të rregullt përcaktohet si produkt i gjysmëperimetrit të bazës dhe apotemës.

Dëshmi.

Le të shënojmë anën e bazës së piramidës $n-$gonale me $a$ dhe apotemën me $d$. Prandaj, zona e fytyrës anësore është e barabartë me

Meqenëse, sipas Teoremës 1, të gjitha anët janë të barabarta, atëherë

Teorema është vërtetuar.

Një lloj tjetër piramide është një piramidë e cunguar.

Përkufizimi 4

Nëse një rrafsh paralel me bazën e tij tërhiqet përmes një piramide të zakonshme, atëherë figura e formuar midis këtij rrafshi dhe rrafshit të bazës quhet piramidë e cunguar (Fig. 5).

Figura 5. Piramida e cunguar

Faqet anësore të piramidës së cunguar janë trapezoide.

Teorema 3

Sipërfaqja anësore e një piramide të rregullt të cunguar përcaktohet si produkt i shumës së gjysmëperimetrave të bazave dhe apotemës.

Dëshmi.

Le t'i shënojmë anët e bazave të piramidës $n-$gonale me përkatësisht $a\ dhe\ b$ dhe apotemën me $d$. Prandaj, zona e fytyrës anësore është e barabartë me

Meqenëse të gjitha anët janë të barabarta, atëherë

Teorema është vërtetuar.

Shembull i detyrës

Shembulli 1

Gjeni sipërfaqen e sipërfaqes anësore të një piramide trekëndore të cunguar nëse ajo është marrë nga një piramidë e rregullt me ​​anën bazë 4 dhe apotemën 5 duke prerë një rrafsh që kalon përmes vijës së mesme të faqeve anësore.

Zgjidhje.

Duke përdorur teoremën e vijës së mesme, gjejmë se baza e sipërme e piramidës së cunguar është e barabartë me $4\cdot \frac(1)(2)=2$, dhe apotema është e barabartë me $5\cdot \frac(1)(2) = 2,5 dollarë.

Pastaj, nga teorema 3, marrim

Përkufizimi

Piramidaështë një shumëfaqësh i përbërë nga një shumëkëndësh \(A_1A_2...A_n\) dhe \(n\) trekëndësha me një kulm të përbashkët \(P\) (jo i shtrirë në rrafshin e shumëkëndëshit) dhe brinjë përballë tij, që përkojnë me anët e shumëkëndëshit.
Përcaktimi: \(PA_1A_2...A_n\) .
Shembull: piramida pesëkëndore \(PA_1A_2A_3A_4A_5\) .

Trekëndëshat \(PA_1A_2, \PA_2A_3\), etj. quhen fytyrat anësore piramidat, segmentet \(PA_1, PA_2\), etj. - brinjë anësore, shumëkëndësh \(A_1A_2A_3A_4A_5\) - bazë, pika \(P\) - krye.

Lartësia piramidat janë një pingul i zbritur nga maja e piramidës në rrafshin e bazës.

Një piramidë me një trekëndësh në bazën e saj quhet katërkëndësh.

Piramida quhet e saktë, nëse baza e tij është një shumëkëndësh i rregullt dhe plotësohet një nga kushtet e mëposhtme:

\((a)\) skajet anësore të piramidës janë të barabarta;

\((b)\) lartësia e piramidës kalon nëpër qendrën e rrethit të rrethuar pranë bazës;

\((c)\) brinjët anësore janë të prirura në rrafshin e bazës në të njëjtin kënd.

\((d)\) faqet anësore janë të prirura në rrafshin e bazës në të njëjtin kënd.

Tetraedron i rregulltështë një piramidë trekëndore, të gjitha faqet e së cilës janë trekëndësha barabrinjës të barabartë.

Teorema

Kushtet \((a), (b), (c), (d)\) janë ekuivalente.

Dëshmi

Le të gjejmë lartësinë e piramidës \(PH\) . Le të jetë \(\alfa\) rrafshi i bazës së piramidës.

1) Le të vërtetojmë se nga \((a)\) rrjedh \((b)\) . Le të \(PA_1=PA_2=PA_3=...=PA_n\) .

Sepse \(PH\perp \alpha\), atëherë \(PH\) është pingul me çdo vijë që shtrihet në këtë plan, që do të thotë se trekëndëshat janë kënddrejtë. Kjo do të thotë që këta trekëndësha janë të barabartë në këmbën e përbashkët \(PH\) dhe hipotenuzë \(PA_1=PA_2=PA_3=...=PA_n\) . Kjo do të thotë \(A_1H=A_2H=...=A_nH\) . Kjo do të thotë se pikat \(A_1, A_2, ..., A_n\) janë në të njëjtën distancë nga pika \(H\), prandaj, ato shtrihen në të njëjtin rreth me rreze \(A_1H\) . Ky rreth, sipas përkufizimit, është i rrethuar rreth shumëkëndëshit \(A_1A_2...A_n\) .

2) Le të vërtetojmë se \((b)\) nënkupton \((c)\) .

\(PA_1H, PA_2H, PA_3H,..., PA_nH\) drejtkëndëshe dhe e barabartë në dy këmbë. Kjo do të thotë se këndet e tyre janë gjithashtu të barabarta, prandaj, \(\këndi PA_1H=\këndi PA_2H=...=\këndi PA_nH\).

3) Le të vërtetojmë se \((c)\) nënkupton \((a)\) .

Ngjashëm me pikën e parë, trekëndëshat \(PA_1H, PA_2H, PA_3H,..., PA_nH\) drejtkëndëshe si përgjatë këmbës ashtu edhe këndi akut. Kjo do të thotë se edhe hipotenuset e tyre janë të barabarta, pra \(PA_1=PA_2=PA_3=...=PA_n\) .

4) Le të vërtetojmë se \((b)\) nënkupton \((d)\) .

Sepse në një shumëkëndësh të rregullt qendrat e rrathëve të rrethuar dhe të brendashkruar përkojnë (në përgjithësi, kjo pikë quhet qendra e një shumëkëndëshi të rregullt), atëherë \(H\) është qendra e rrethit të brendashkruar. Le të vizatojmë pingulet nga pika \(H\) në anët e bazës: \(HK_1, HK_2\), etj. Këto janë rrezet e rrethit të brendashkruar (sipas përkufizimit). Pastaj, sipas TTP (\(PH\) është pingul me planin, \(HK_1, HK_2\), etj. janë projeksione pingul me anët) të pjerrëta \(PK_1, PK_2\), etj. pingul me brinjët \(A_1A_2, A_2A_3\), etj. përkatësisht. Pra, sipas përkufizimit \(\këndi PK_1H, \këndi PK_2H\) të barabartë me këndet ndërmjet faqeve anësore dhe bazës. Sepse trekëndëshat \(PK_1H, PK_2H, ...\) janë të barabartë (si drejtkëndëshe në dy anët), pastaj këndet \(\këndi PK_1H, \këndi PK_2H, ...\) janë të barabartë.

5) Le të vërtetojmë se \((d)\) nënkupton \((b)\) .

Ngjashëm me pikën e katërt, trekëndëshat \(PK_1H, PK_2H, ...\) janë të barabartë (si drejtkëndësh përgjatë këmbës dhe këndi akut), që do të thotë se segmentet \(HK_1=HK_2=...=HK_n\) janë të barabartë. Kjo do të thotë, sipas përkufizimit, \(H\) është qendra e një rrethi të gdhendur në bazë. Por sepse Për shumëkëndëshat e rregullt, qendrat e rrathëve të brendashkruar dhe të rrethuar përputhen, atëherë \(H\) është qendra e rrethit të rrethuar. Chtd.

Pasoja

Faqet anësore të një piramide të rregullt janë trekëndësha të barabartë dykëndësh.

Përkufizimi

Lartësia e faqes anësore të një piramide të rregullt të nxjerrë nga kulmi i saj quhet apotemë.
Apotemat e të gjitha faqeve anësore të një piramide të rregullt janë të barabarta me njëra-tjetrën dhe janë gjithashtu mediana dhe përgjysmues.

Shënime të rëndësishme

1. Lartësia e një piramide të rregullt trekëndore bie në pikën e kryqëzimit të lartësive (ose përgjysmuesve, ose medianave) të bazës (baza është një trekëndësh i rregullt).

2. Lartësia e një piramide të rregullt katërkëndore bie në pikën e prerjes së diagonaleve të bazës (baza është katror).

3. Lartësia e një piramide të rregullt gjashtëkëndore bie në pikën e kryqëzimit të diagonaleve të bazës (baza është një gjashtëkëndësh i rregullt).

4. Lartësia e piramidës është pingul me çdo vijë të drejtë që shtrihet në bazë.

Përkufizimi

Piramida quhet drejtkëndëshe, nëse njëra nga skajet anësore të saj është pingul me rrafshin e bazës.

Shënime të rëndësishme

1. Në një piramidë drejtkëndore, skaji pingul me bazën është lartësia e piramidës. Kjo do të thotë, \(SR\) është lartësia.

2. Sepse \(SR\) është pingul me çdo vijë nga baza, atëherë \(\trekëndëshi SRM, \trekëndëshi SRP\)– trekëndëshat kënddrejtë.

3. Trekëndëshat \(\trekëndësh SRN, \trekëndësh SRK\)- gjithashtu drejtkëndëshe.
Kjo do të thotë, çdo trekëndësh i formuar nga ky skaj dhe diagonalja që del nga kulmi i kësaj skaji që shtrihet në bazë do të jetë drejtkëndëshe.

\[(\Large(\tekst(Vëllimi dhe sipërfaqja e piramidës)))\]

Teorema

Vëllimi i piramidës është i barabartë me një të tretën e produktit të sipërfaqes së bazës dhe lartësisë së piramidës: \

Pasojat

Le të jetë \(a\) ana e bazës, \(h\) lartësia e piramidës.

1. Vëllimi i një piramide të rregullt trekëndore është \(V_(\text(trekëndëshi djathtas.pir.))=\dfrac(\sqrt3)(12)a^2h\),

2. Vëllimi i një piramide të rregullt katërkëndore është \(V_(\text(djathtas.katër.pir.))=\dfrac13a^2h\).

3. Vëllimi i një piramide të rregullt gjashtëkëndore është \(V_(\text(djathtas.six.pir.))=\dfrac(\sqrt3)(2)a^2h\).

4. Vëllimi i një tetraedri të rregullt është \(V_(\tekst(tetr. djathtas))=\dfrac(\sqrt3)(12)a^3\).

Teorema

Sipërfaqja e sipërfaqes anësore të një piramide të rregullt është e barabartë me gjysmën e produktit të perimetrit të bazës dhe apotemës.

\[(\Large(\tekst(Frustum)))\]

Përkufizimi

Konsideroni një piramidë arbitrare \(PA_1A_2A_3...A_n\) . Le të vizatojmë një rrafsh paralel me bazën e piramidës përmes një pike të caktuar që shtrihet në skajin anësor të piramidës. Ky plan do ta ndajë piramidën në dy poliedra, njëra prej të cilave është një piramidë (\(PB_1B_2...B_n\)), dhe tjetra quhet piramidë e cunguar(\(A_1A_2...A_nB_1B_2...B_n\) ).

Piramida e cunguar ka dy baza - shumëkëndëshat \(A_1A_2...A_n\) dhe \(B_1B_2...B_n\) të cilat janë të ngjashme me njëri-tjetrin.

Lartësia e një piramide të cunguar është një pingul i tërhequr nga një pikë e bazës së sipërme në rrafshin e bazës së poshtme.

Shënime të rëndësishme

1. Të gjitha faqet anësore të një piramide të cunguar janë trapezoide.

2. Segmenti që lidh qendrat e bazave të një piramide të rregullt të cunguar (domethënë një piramidë e përftuar nga prerja tërthore e një piramide të rregullt) është lartësia.

Kur një person dëgjon fjalën "piramidë", ai kujton menjëherë strukturat madhështore egjiptiane. Sidoqoftë, gjigantët e lashtë prej guri janë vetëm një nga përfaqësuesit e klasës piramidale. Në këtë artikull ne do të shqyrtojmë nga një këndvështrim gjeometrik vetitë e një piramide të rregullt katërkëndore.

Çfarë është një piramidë në përgjithësi?

Në gjeometri, kuptohet si një figurë tredimensionale, e cila mund të merret duke lidhur të gjitha kulmet e një shumëkëndëshi të sheshtë me një pikë të vetme që shtrihet në një rrafsh të ndryshëm nga ky shumëkëndësh. Figura më poshtë tregon 4 forma që plotësojnë këtë përkufizim.

Shohim që figura e parë ka një bazë trekëndore, e dyta ka një bazë katërkëndëshe. Dy të fundit përfaqësohen nga një bazë pesëkëndëshe dhe gjashtëkëndore. Sidoqoftë, sipërfaqja anësore e të gjitha piramidave është e formuar nga trekëndësha. Numri i tyre është saktësisht i barabartë me numrin e brinjëve ose kulmeve të shumëkëndëshit në bazë.

Një lloj i veçantë piramide, i cili ndryshon nga përfaqësuesit e tjerë të klasës në simetrinë e saj ideale, është piramida e rregullt. Që shifra të jetë e saktë, duhet të plotësohen dy parakushtet e mëposhtme:

• baza duhet të ketë një shumëkëndësh të rregullt;
• sipërfaqja anësore e figurës duhet të përbëhet nga trekëndësha të barabartë dykëndësh.

Vini re se kushti i dytë i detyrueshëm mund të zëvendësohet nga një tjetër: një pingul i tërhequr në bazë nga maja e piramidës (pika e kryqëzimit të trekëndëshave anësor) duhet të presë këtë bazë në qendrën e saj gjeometrike.

Tani le të kalojmë në temën e artikullit dhe të shqyrtojmë se cilat veti të një piramide të rregullt katërkëndore e karakterizojnë atë. Së pari, le të tregojmë në figurë se si duket kjo figurë.

Baza e saj është një katror. Brinjët përfaqësojnë 4 trekëndësha identikë dykëndësh (mund të jenë edhe barabrinjës në një raport të caktuar të gjatësisë së brinjës së katrorit dhe lartësisë së figurës). Lartësia e ulur nga maja e piramidës do të presë sheshin në qendër të saj (pika e kryqëzimit të diagonaleve).

Kjo piramidë ka 5 faqe (një katror dhe katër trekëndësha), 5 kulme (katër prej tyre i përkasin bazës) dhe 8 skaje. rendi i katërt, duke kaluar nëpër lartësinë e piramidës, e shndërron atë në vetvete duke e rrotulluar 90 o.

Piramidat egjiptiane në Giza janë të rregullta katërkëndëshe.

Katër parametra linearë bazë

Le të fillojmë shqyrtimin tonë të vetive matematikore të një piramide të rregullt katërkëndore me formulat për lartësinë, gjatësinë anësore të bazës, skajin anësor dhe apotemën. Le të themi menjëherë se të gjitha këto sasi janë të lidhura me njëra-tjetrën, kështu që mjafton të njihni vetëm dy prej tyre për të llogaritur pa mëdyshje dy të tjerat.

Supozoni se dihet lartësia h e piramidës dhe gjatësia a e anës së bazës katrore, atëherë buza anësore b do të jetë e barabartë me:

b = √(a 2 / 2 + h 2)

Tani japim formulën për gjatësinë a b të apotemës (lartësia e trekëndëshit të ulur në anën e bazës):

a b = √(a 2 / 4 + h 2)

Natyrisht, buza anësore b është gjithmonë më e madhe se apotema a b.

Të dyja shprehjet mund të përdoren për të përcaktuar të katër karakteristikat lineare nëse dihen dy parametrat e tjerë, për shembull a b dhe h.

Sipërfaqja dhe vëllimi i një figure

Këto janë dy veti më të rëndësishme të një piramide të rregullt katërkëndore. Baza e figurës ka zonën e mëposhtme:

Çdo nxënës e di këtë formulë. Sipërfaqja e sipërfaqes anësore, e cila formohet nga katër trekëndësha identikë, mund të përcaktohet përmes apotemës a b të piramidës si më poshtë:

Nëse a b është i panjohur, atëherë mund të përcaktohet duke përdorur formulat nga paragrafi i mëparshëm përmes lartësisë h ose skajit b.

Sipërfaqja totale e figurës në shqyrtim është shuma e sipërfaqeve S o dhe S b:

S = S o + S b = a 2 + 2 × a × a b = a (a + 2 × a b)

Zona e llogaritur e të gjitha fytyrave të piramidës është paraqitur në figurën më poshtë në formën e zhvillimit të saj.

Një përshkrim i vetive të një piramide të rregullt katërkëndore nuk do të jetë i plotë pa marrë parasysh formulën për përcaktimin e vëllimit të saj. Kjo vlerë për piramidën në fjalë llogaritet si më poshtë:

Kjo do të thotë, V është e barabartë me pjesën e tretë të produktit të lartësisë së figurës dhe sipërfaqes së bazës së saj.

Vetitë e një piramide të rregullt katërkëndore të cunguar

Ju mund ta merrni këtë shifër nga piramida origjinale. Për ta bërë këtë, ju duhet të prisni majën e piramidës me një aeroplan. Figura e mbetur nën rrafshin e prerë do të quhet një piramidë e cunguar.

Është më e përshtatshme për të studiuar karakteristikat e një piramide të cunguar nëse bazat e saj janë paralele me njëra-tjetrën. Në këtë rast, bazat e poshtme dhe të sipërme do të jenë shumëkëndësha të ngjashëm. Meqenëse në një piramidë të rregullt katërkëndore baza është një katror, ​​pjesa e formuar gjatë prerjes do të përfaqësojë gjithashtu një katror, ​​por me përmasa më të vogla.

Sipërfaqja anësore e figurës së cunguar nuk formohet nga trekëndësha, por nga trapezoide izoscele.

Një nga vetitë e rëndësishme të kësaj piramide është vëllimi i saj, i cili llogaritet me formulën:

V = 1/3 × h × (S o1 + S o2 + √(S o1 × S o2))

Këtu h është distanca midis bazave të figurës, S o1, S o2 janë zonat e bazave të poshtme dhe të sipërme.

Një piramidë është një shumëfaqësh me një shumëkëndësh në bazën e saj. Të gjitha fytyrat, nga ana tjetër, formojnë trekëndësha që konvergojnë në një kulm. Piramidat janë trekëndore, katërkëndore, etj. Për të përcaktuar se cila piramidë është para jush, mjafton të numëroni numrin e këndeve në bazën e saj. Përkufizimi i "lartësisë së një piramide" gjendet shumë shpesh në problemet e gjeometrisë në kurrikulën shkollore. Në këtë artikull do të përpiqemi të shohim mënyra të ndryshme për ta gjetur atë.

Pjesë të piramidës

Çdo piramidë përbëhet nga elementët e mëposhtëm:

• faqe anësore, të cilat kanë tre qoshe dhe konvergojnë në majë;
• apotema përfaqëson lartësinë që zbret nga maja e saj;
• maja e piramidës është një pikë që lidh brinjët anësore, por nuk shtrihet në rrafshin e bazës;
• baza është një shumëkëndësh mbi të cilin kulmi nuk shtrihet;
• lartësia e një piramide është një segment që kryqëzon majën e piramidës dhe formon një kënd të drejtë me bazën e saj.

Si të gjeni lartësinë e një piramide nëse dihet vëllimi i saj

Përmes formulës V = (S*h)/3 (në formulën V është vëllimi, S është sipërfaqja e bazës, h është lartësia e piramidës) gjejmë se h = (3*V)/ S. Për të konsoliduar materialin, le ta zgjidhim menjëherë problemin. Baza trekëndore është 50 cm 2 , ndërsa vëllimi i saj është 125 cm 3 . Lartësia e piramidës trekëndore është e panjohur, gjë që duhet të gjejmë. Gjithçka është e thjeshtë këtu: ne futim të dhënat në formulën tonë. Marrim h = (3*125)/50 = 7,5 cm.

Si të gjeni lartësinë e një piramide nëse dihen gjatësia e diagonales dhe skajet e saj

Siç e kujtojmë, lartësia e piramidës formon një kënd të drejtë me bazën e saj. Kjo do të thotë se lartësia, skaji dhe gjysma e diagonales së bashku formojnë Shumë, natyrisht, mbajnë mend teoremën e Pitagorës. Duke ditur dy dimensione, nuk do të jetë e vështirë të gjesh sasinë e tretë. Le të kujtojmë teoremën e njohur a² = b² + c², ku a është hipotenuza, dhe në rastin tonë skaji i piramidës; b - këmbën e parë ose gjysmën e diagonales dhe c - përkatësisht, këmbën e dytë, ose lartësinë e piramidës. Nga kjo formulë c² = a² - b².

Tani problemi: në një piramidë të rregullt diagonalja është 20 cm, kur gjatësia e skajit është 30 cm. Duhet të gjeni lartësinë. Ne zgjidhim: c² = 30² - 20² = 900-400 = 500. Prandaj c = √ 500 = rreth 22.4.

Si të gjeni lartësinë e një piramide të cunguar

Ai është një shumëkëndësh me një seksion kryq paralel me bazën e tij. Lartësia e një piramide të cunguar është segmenti që lidh dy bazat e saj. Lartësia mund të gjendet për një piramidë të rregullt nëse dihen gjatësitë e diagonaleve të të dy bazave, si dhe skaji i piramidës. Le të jetë diagonalja e bazës më të madhe d1, ndërsa diagonalja e bazës më të vogël është d2, dhe skaji ka gjatësi l. Për të gjetur lartësinë, mund të ulni lartësitë nga dy pikat e sipërme të kundërta të diagramit në bazën e saj. Ne shohim se kemi dy trekëndësha kënddrejtë; gjithçka që mbetet është të gjejmë gjatësinë e këmbëve të tyre. Për ta bërë këtë, zbritni atë më të vogël nga diagonalja më e madhe dhe ndani me 2. Kështu do të gjejmë njërën këmbë: a = (d1-d2)/2. Pas së cilës, sipas teoremës së Pitagorës, gjithçka që duhet të bëjmë është të gjejmë këmbën e dytë, që është lartësia e piramidës.

Tani le ta shohim të gjithë këtë në praktikë. Ne kemi një detyrë përpara. Një piramidë e cunguar ka një katror në bazë, gjatësia diagonale e bazës më të madhe është 10 cm, ndërsa ajo më e vogël është 6 cm, dhe buza është 4 cm. Ju duhet të gjeni lartësinë. Së pari, gjejmë një këmbë: a = (10-6)/2 = 2 cm Një këmbë është e barabartë me 2 cm, dhe hipotenuza është 4 cm. Rezulton se këmba e dytë ose lartësia do të jetë e barabartë me 16- 4 = 12, domethënë h = √12 = rreth 3,5 cm.

Gjatë zgjidhjes së problemit C2 duke përdorur metodën e koordinatave, shumë nxënës përballen me të njëjtin problem. Ata nuk mund të llogarisin koordinatat e pikave të përfshira në formulën e produktit skalar. Vështirësitë më të mëdha lindin piramidat. Dhe nëse pikat bazë konsiderohen pak a shumë normale, atëherë majat janë një ferr i vërtetë.

Sot do të punojmë në një piramidë të rregullt katërkëndore. Ekziston edhe një piramidë trekëndore (aka - katërkëndësh). Ky është një dizajn më kompleks, kështu që do t'i kushtohet një mësim i veçantë.

Së pari, le të kujtojmë përkufizimin:

Një piramidë e rregullt është ajo që:

1. Baza është një shumëkëndësh i rregullt: trekëndësh, katror, ​​etj.;
2. Një lartësi e tërhequr nga baza kalon përmes qendrës së saj.

Në veçanti, baza e një piramide katërkëndore është katrore. Ashtu si Keopsi, vetëm pak më i vogël.

Më poshtë janë llogaritjet për një piramidë në të cilën të gjitha skajet janë të barabarta me 1. Nëse nuk është kështu në problemin tuaj, llogaritjet nuk ndryshojnë - thjesht numrat do të jenë të ndryshëm.

Kulmet e një piramide katërkëndore

Pra, le të jepet një piramidë e rregullt katërkëndore SABCD, ku S është kulmi dhe baza ABCD është katror. Të gjitha skajet janë të barabarta me 1. Duhet të futni një sistem koordinativ dhe të gjeni koordinatat e të gjitha pikave. Ne kemi:

Ne prezantojmë një sistem koordinativ me origjinë në pikën A:

1. Boshti OX drejtohet paralel me skajin AB;
2. Boshti OY është paralel me AD. Meqenëse ABCD është katror, ​​AB ⊥ AD;
3. Së fundi, ne e drejtojmë boshtin OZ lart, pingul me rrafshin ABCD.

Tani llogarisim koordinatat. Ndërtimi shtesë: SH - lartësia e tërhequr në bazë. Për lehtësi, ne do të vendosim bazën e piramidës në një vizatim të veçantë. Meqenëse pikat A, B, C dhe D shtrihen në rrafshin OXY, koordinata e tyre është z = 0. Kemi:

1. A = (0; 0; 0) - përkon me origjinën;
2. B = (1; 0; 0) - hap pas 1 përgjatë boshtit OX nga origjina;
3. C = (1; 1; 0) - hap me 1 përgjatë boshtit OX dhe me 1 përgjatë boshtit OY;
4. D = (0; 1; 0) - hap vetëm përgjatë boshtit OY.
5. H = (0.5; 0.5; 0) - qendra e sheshit, mesi i segmentit AC.

Mbetet për të gjetur koordinatat e pikës S. Vini re se koordinatat x dhe y të pikave S dhe H janë të njëjta, pasi ato shtrihen në një vijë paralele me boshtin OZ. Mbetet për të gjetur koordinatën z për pikën S.

Merrni parasysh trekëndëshat ASH dhe ABH:

1. AS = AB = 1 sipas kushtit;
2. Këndi AHS = AHB = 90°, pasi SH është lartësia dhe AH ⊥ HB si diagonale të katrorit;
3. Ana AH është e zakonshme.

Prandaj, trekëndëshat kënddrejtë ASH dhe ABH të barabartë një këmbë dhe një hipotenuzë secila. Kjo do të thotë SH = BH = 0,5 BD. Por BD është diagonalja e një katrori me brinjën 1. Prandaj kemi:

Koordinatat totale të pikës S:

Si përfundim, ne shkruajmë koordinatat e të gjitha kulmeve të një piramide të rregullt drejtkëndore:

Çfarë duhet të bëni kur brinjët janë të ndryshme

Po sikur skajet anësore të piramidës të mos jenë të barabarta me skajet e bazës? Në këtë rast, merrni parasysh trekëndëshin AHS:

Trekëndëshi AHS - drejtkëndëshe, dhe hipotenuza AS është gjithashtu një skaj anësor i piramidës origjinale SABCD. Këmba AH llogaritet lehtësisht: AH = 0,5 AC. Do të gjejmë këmbën e mbetur SH sipas teoremës së Pitagorës. Kjo do të jetë koordinata z për pikën S.

Detyrë. Jepet një piramidë e rregullt katërkëndore SABCD, në bazën e së cilës shtrihet një katror me brinjë 1. Buza anësore BS = 3. Gjeni koordinatat e pikës S.

Ne tashmë i dimë koordinatat x dhe y të kësaj pike: x = y = 0,5. Kjo rrjedh nga dy fakte:

1. Projeksioni i pikës S në rrafshin OXY është pika H;
2. Në të njëjtën kohë, pika H është qendra e një katrori ABCD, të gjitha anët e të cilit janë të barabarta me 1.

Mbetet për të gjetur koordinatat e pikës S. Merrni parasysh trekëndëshin AHS. Është drejtkëndëshe, me hipotenuzë AS = BS = 3, këmbën AH është gjysma e diagonales. Për llogaritjet e mëtejshme na duhet gjatësia e saj:

Teorema e Pitagorës për trekëndëshin AHS: AH 2 + SH 2 = AS 2. Ne kemi:

Pra, koordinatat e pikës S: